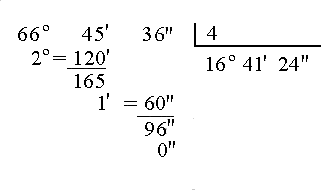Plantilla:Operaciones con ángulos
De Wikipedia
| Revisión de 09:02 7 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:03 7 may 2017 Coordinador (Discusión | contribuciones) (→Resta) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| {{p}} | {{p}} | ||
| ===Resta=== | ===Resta=== | ||
| - | Para restar tendremos en cuenta las mismas consideraciones que para sumar. Analicemos el siguiente ejemplo: | + | {{resta de ángulos}} |
| - | + | ||
| - | {{Ejemplo | + | |
| - | |titulo=Ejemplo: ''Resta en el sistema sexagesimal'' | + | |
| - | |enunciado= | + | |
| - | :En la primera carrera, Luis había tardado 2 h 48 min 35 s y su compañero corrió la maratón en 3 horas exactamente. ¿Cuál es la diferencia de tiempo entre ambos? | + | |
| - | |sol= | + | |
| - | Debemos hacer la siguiente operación: | + | |
| - | + | ||
| - | <center><pre> | + | |
| - | 3 h 0 min 0 s | + | |
| - | − 2 h 48 min 35 s | + | |
| - | ___________________ | + | |
| - | + | ||
| - | </pre></center> | + | |
| - | + | ||
| - | Igual que en la suma, deberíamos restar por separado las horas los minutos y los segundos, pero no podemos hacer las restas 0-35 (segundos) ni 0-48 (minutos). Para conseguirlo transformamos una hora en 60 minutos y un minuto en 60 segundos. Es decir, las 3 horas se convierten en 2h 59' 60". | + | |
| - | + | ||
| - | <center><pre> | + | |
| - | 2 h 60 min 60 s | + | |
| - | − 2 h 48 min 35 s | + | |
| - | ___________________ | + | |
| - | 0 h 11 min 25 s | + | |
| - | </pre></center> | + | |
| - | }} | + | |
| - | + | ||
| - | {{p}} | + | |
| - | {{AI_enlace|titulo1=Actividad Interactiva: ''Resta de ángulos'' | + | |
| - | |descripcion=Realiza en tu cuaderno las siguientes restas de ángulos: | + | |
| - | + | ||
| - | :a) 56º 20' 40" - 37º 42' 15" | + | |
| - | + | ||
| - | :b) 125º 15' 30" - 24º 50' 40" | + | |
| - | + | ||
| - | :c) 33º 33' 33" - 17º 43' 34" | + | |
| - | |url1=http://proyectodescartes.org/uudd/materiales_didacticos/Medicion_de_angulos-JS/angulo6.htm | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | {{AI_enlace|titulo1=Actividad Interactiva: ''Ángulos complementarios y suplementarios'' | + | |
| - | |descripcion=Calcula los ángulos complementario y suplementario de los siguientes: | + | |
| - | + | ||
| - | :a) 56º 20' 40" | + | |
| - | + | ||
| - | :b) 37º 42' 15" | + | |
| - | + | ||
| - | :c) 125º 15' 30" | + | |
| - | |url1=http://proyectodescartes.org/uudd/materiales_didacticos/Medicion_de_angulos-JS/angulo9.htm | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | {{Video_enlace_julioprofe | + | |
| - | |titulo1=Ejemplo 1 | + | |
| - | |duracion=3'45" | + | |
| - | |sinopsis=¿Cuál es el complementario de 53º41'28" | + | |
| - | |url1=https://www.youtube.com/watch?v=zIUtvfczPa8 | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace_julioprofe | + | |
| - | |titulo1=Ejemplo 2 | + | |
| - | |duracion=3'43" | + | |
| - | |sinopsis=¿Cuál es el suplementario de 75º16'49" | + | |
| - | |url1=https://www.youtube.com/watch?v=UVxyZ0-8MDY | + | |
| - | }} | + | |
| ===Multiplicación por un número natural=== | ===Multiplicación por un número natural=== | ||
Revisión de 09:03 7 may 2017
Operaciones con ángulos Descripción: En esta escena podrás ver como se opera con ángulos gráficamente y algebraicamente.
Tabla de contenidos |
Suma
Dos o más ángulos pueden sumarse para formar otro. La operación suma de ángulos se realiza tanto gráficamente como analíticamente:
- La suma gráfica se realiza colocando los ángulos en posición de consecutivos, es decir, compartiendo el vértice y un lado, para dar lugar a otro ángulo que comprende a ambos.
- La suma analítica se realiza sumando las amplitudes de los ángulos para obtener la amplitud del ángulo resultante.
Suma de ángulos Descripción: Actividad en la que podrás ver como se suman ángulos gráficamente y de forma analítica en forma simple. Podrás hacer uso de un transportador de ángulos virtual para comprobar los resultados.
Suma de ángulos Descripción: Construcción gráfica de la suma de dos ángulos, con regla y compás.
Procedimiento
Para sumar analíticamente un ángulos en sexagesimal, en forma compleja:
- Sumamos cada una de las unidades del ángulo (grados, minutos y segundos).
- Si la suma de los segundos es superior a 60, la transformamos en minutos, y se la añadimos a los minutos.
- Si la suma de los minutos es superior a 60, la transformamos en grados, y se la añadimos a los grados.
Ejemplo: Suma de ángulos
Calcula la siguiente suma de ángulo en sexagesimal en forma compleja:
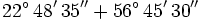
Solución:
Si sumamos por separado los grados, los minutos y los segundos, resulta:
22º 48' 35" + 56º 45' 30" _______________ 78º 93' 65"
Pero 65" equivalen a 1' (60") y 5", luego la suma se puede escribir así:
78º 94' 5"
De la misma forma, 94' equivalen a 1º (60') y 34'. Luego la suma es:
79º 34' 5"
Actividad 1 Descripción: Realiza en tu cuaderno las siguientes sumas de ángulos en sexagesimal en forma compleja y comprueba los resultados pinchando en el enlace de arriba:
- a) 56º 20' 40" + 37º 42' 15"
- b) 125º 15' 30" + 24º 50' 40"
- c) 33º 33' 33" + 17º 43' 34"
Actividad 2 Descripción: Suma de ángulos en sexagesimal.
Tutorial (6'25") Sinopsis:Suma de ángulos en forma compleja.
Ejercicio 1 (3'37") Sinopsis: Calcula: (26º 42' 51") + (11º 30' 14")
Ejercicio 2 (2'48") Sinopsis: Calcula: (26º 14' 41") + (24º 59")
Ejercicio 3 (2'42") Sinopsis: Calcula: (38º 47') + (19º 54' 10")
Resta
La resta o diferencia de ángulos puede hacerse, igual que la suma, de dos formas: gráfica y analítica.
- La resta gráfica, consiste en colocar los dos ángulos de manera que compartan el vértice y un lado. Así, el ángulo mayor comprende al menor, y el exceso es la diferencia entre ambos.
- La resta analítica se realiza restando la amplitud del ángulo menor de la del mayor.
Resta de ángulos Descripción: Actividad en la que podrás ver como se restan ángulos de forma gráfica y de forma analítica simple. Podrás hacer uso de un transportador de ángulos virtual para comprobar los resultados.
Resta de ángulos Descripción: Construcción gráfica de la resta de dos ángulos, con regla y compás.
Procedimiento
Para restar analíticamente ángulos en sexagesimal, en forma compleja:
- Restamos cada una de las unidades del ángulo (grados, minutos y segundos).
- Si al restar los segundos, el minuendo es menor que el sustraendo, transformaremos un minuto en 60" y se lo sumaremos a los segundos.
- Si al restar los minutos, el minuendo es menor que el sustraendo, transformaremos un grado en 60' y se lo sumaremos a los minutos.
- Terminaremos restando los grados normalmente.
Veamos un ejemplo:
Ejemplo: Resta de ángulos
Calcula la siguiente resta de ángulo en sexagesimal en forma compleja :
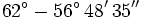
Debemos hacer la siguiente operación:
62º 0' 0" − 56º 48' 35" _______________
Igual que en la suma, deberíamos restar por separado las horas los minutos y los segundos, pero no podemos hacer las restas 0-35 (segundos) ni 0-48 (minutos). Para conseguirlo transformamos una grado en 60 minutos y un minuto en 60 segundos. Es decir, los 60º se convierten en 61º 59' 60".
61º 59' 60" − 56º 48' 35" _____________ 5º 11' 25"
Actividad 1 Descripción: Realiza en tu cuaderno las siguientes restas de ángulos en sexagesimal en forma compleja y comprueba los resultados pinchando en el enlace de arriba:
- a) 56º 20' 40" - 37º 42' 15"
- b) 125º 15' 30" - 24º 50' 40"
- c) 33º 33' 33" - 17º 43' 34"
Actividad 2 Descripción: Calcula el complementario y el suplementario de los siguientes ángulos y comprueba los resultados pinchando en el enlace de arriba:
- a) 56º 20' 40"
- b) 37º 42' 15"
- c) 125º 15' 30"
Actividad 3 Descripción: Resta de ángulos en sexagesimal.
Actividad 4 Descripción: Resta de ángulos en sexagesimal.
Actividad 5 Descripción: Cálculo del complementario y del suplementario.
Actividad 6 Descripción: Cálculo del complementario y del suplementario.
Tutorial (5'08") Sinopsis:Resta de ángulos en forma compleja.
Ejercicio 1 (2'58") Sinopsis: Calcula: (213º 17' 25") - (122º 35' 48")
Ejercicio 2 (2'52") Sinopsis: Calcula: (49º 12') - (15º 27' 50")
Ejercicio 3 (2'16") Sinopsis: Calcula: (100º 18") - (31º 20' 10")
Ejercicio 4 (2'55") Sinopsis: Calcula: (147º) - (23º 52' 3")
Ejercicio 5 (3'45") Sinopsis: ¿Cuál es el complementario de 53º41'28"
Ejercicio 6 (3'43") Sinopsis: ¿Cuál es el suplementario de 75º16'49"
Ejercicio 7 (2'34") Sinopsis:Calcula: (131º 45' 36") - (31º 58' 26")
Tutorial 1 (7'37") Sinopsis:Suma y resta de ángulos en forma compleja, en el sistema sexagesimal.
Tutorial 2 (2'12") Sinopsis:Suma y resta de ángulos en forma compleja, en el sistema sexagesimal.
Multiplicación por un número natural
Para multiplicar un ángulo por un número natural debemos multiplicar por ese número cada una de las unidades del ángulo (grados, minutos y segundos). Si alguno de los productos de los segundos o minutos es superior a 60, lo transformamos en una unidad de orden inmediatamente superior.
Analicemos el siguiente ejemplo:
Ejemplo: Producto por un número en el sistema sexagesimal
- Multiplica 18º 26' 35" por 3.
18º 26' 35" x 3 _______________ 54º 78' 105"
Pero 105" = 1' 45", luego
54º 79' 45"
Pero 79' = 1º 19', luego
55º 19' 45"
Realiza en tu cuaderno las siguientes multiplicaciones de ángulos:
- a) 56º 20' 40" x 2
- b) 37º 42' 15" x 4
- c) 125º 15' 30" x 3
División por un número natural
Para dividir un ángulo por un número natural dividimos los grados entre ese número. Transformamos el resto de la división en minutos, multiplicándolo por 60, y lo sumamos a los que teníamos. Dividimos los minutos. Transformamos el resto de la división en segundos, multiplicándolo por 60, y lo sumamos a los segundos que teníamos. Dividimos los segundos.
Analicemos el siguiente ejemplo:
Ejemplo: División por un número en el sistema sexagesimal
- Divide 66º 45' 36" entre 4.
Realiza en tu cuaderno las siguientes divisiones de ángulos:
- a) 56º 20' 40" : 5
- b) 37º 42' 15" : 4
- c) 125º 15' 30" : 3
