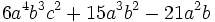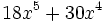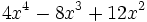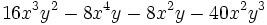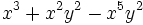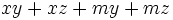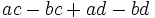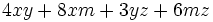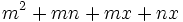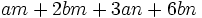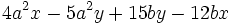Plantilla:Sacar factor común
De Wikipedia
| Revisión de 18:27 29 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:34 29 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 140: | Línea 140: | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| - | |titulo1=Ejercicio 9 | + | |titulo1=Ejercicio 1 |
| |duracion=2'41" | |duracion=2'41" | ||
| |sinopsis=Saca factor común por agrupación de términos: | |sinopsis=Saca factor común por agrupación de términos: | ||
| Línea 149: | Línea 149: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicios 10 | + | |titulo1=Ejercicios 2 |
| |duracion=7'08" | |duracion=7'08" | ||
| |sinopsis=Saca factor común por agrupación de términos: | |sinopsis=Saca factor común por agrupación de términos: | ||
| Línea 156: | Línea 156: | ||
| b) <math>2ac-5bd-2a+2ad+5b-5bc\;</math> | b) <math>2ac-5bd-2a+2ad+5b-5bc\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=uhN2eVLAEDw&index=48&list=PL9B9AC3136D2D4C45}} | + | |url1=https://www.youtube.com/watch?v=uhN2eVLAEDw&index=48&list=PL9B9AC3136D2D4C45 |
| - | + | }} | |
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Ejercicios 11 | + | |titulo1=Ejercicios 3 |
| |duracion=12'37" | |duracion=12'37" | ||
| |sinopsis=Saca factor común por agrupación de términos: | |sinopsis=Saca factor común por agrupación de términos: | ||
| Línea 169: | Línea 169: | ||
| c) <math>x^{n+2}+x^3+x^n+x+x^2+1\;</math> | c) <math>x^{n+2}+x^3+x^n+x+x^2+1\;</math> | ||
| |url1=https://www.youtube.com/watch?v=HLb7Wmx-1_c | |url1=https://www.youtube.com/watch?v=HLb7Wmx-1_c | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=3'20" | ||
| + | |sinopsis=Saca factor común por agrupación de términos: | ||
| + | |||
| + | : <math>xy+xz+my+mz\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=9FkMEiOLCs4&list=PL9SnRnlzoyX0YtiW6G1dZEuM20uYS_wNW&index=8 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=3'31" | ||
| + | |sinopsis=Saca factor común por agrupación de términos: | ||
| + | |||
| + | : <math>ac-bc+ad-bd\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=cviJKF1c1oI&list=PL9SnRnlzoyX0YtiW6G1dZEuM20uYS_wNW&index=9 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=5'14" | ||
| + | |sinopsis=Saca factor común por agrupación de términos: | ||
| + | |||
| + | : <math>4xy+8xm+3yz+6mz\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=ZVHOS1kXrlA&list=PL9SnRnlzoyX0YtiW6G1dZEuM20uYS_wNW&index=10 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=3'40" | ||
| + | |sinopsis=Saca factor común por agrupación de términos: | ||
| + | |||
| + | : <math>m^2+mn+mx+nx\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=H7SGLxExdTk&list=PL9SnRnlzoyX0YtiW6G1dZEuM20uYS_wNW&index=11 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=3'37" | ||
| + | |sinopsis=Saca factor común por agrupación de términos: | ||
| + | |||
| + | : <math>am+2bm+3an+6bn\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=u1BzkYNV5MY&list=PL9SnRnlzoyX0YtiW6G1dZEuM20uYS_wNW&index=12 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=6'02" | ||
| + | |sinopsis=Saca factor común por agrupación de términos: | ||
| + | |||
| + | : <math>4a^2x-5a^2y+15by-12bx\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=UPkMMSMMJUs&index=13&list=PL9SnRnlzoyX0YtiW6G1dZEuM20uYS_wNW | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 18:34 29 may 2017
Sacar factor común en una expresión algebraica con varios sumandos, consiste en encontrar una parte común a todos esos sumandos y aplicar la propiedad distributiva para poner la expresión algebraica como producto de esa parte común y una serie de sumandos entre paréntesis.
Ejemplo: Sacar factor común
Saca factor común en la expresión 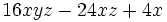
El factor común, que se repite en los tres sumandos, es
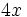 . Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común
. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común 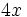 , dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
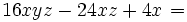
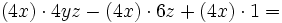
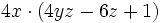
Saca factor común:
a) 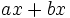
b) 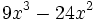
c) 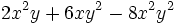
d) 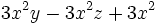
Saca factor común:
a) 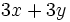
b) 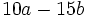
c) 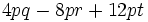
d) 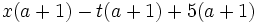
Saca factor común:
a) 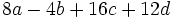
b) 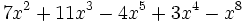
c) 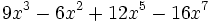
d) 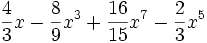
e) 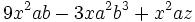
f) 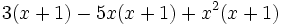
Saca factor común:
a) 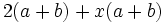
b) 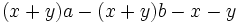
c) 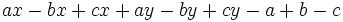
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
a) 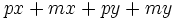
b) 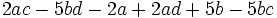
Saca factor común por agrupación de términos:
a) 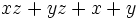
b) 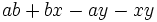
c) 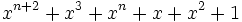
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos: