Plantilla:Racionalizacion
De Wikipedia
| Revisión de 09:24 10 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:05 13 jun 2017 Coordinador (Discusión | contribuciones) (→Actividades) Ir a siguiente diferencia → |
||
| Línea 228: | Línea 228: | ||
| {{Videotutoriales|titulo=Racionalización|enunciado= | {{Videotutoriales|titulo=Racionalización|enunciado= | ||
| {{Video_enlace_unicoos | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejercicios 1 | + | |titulo1=Ejercicio 1 |
| |duracion=7'48" | |duracion=7'48" | ||
| |sinopsis=Racionaliza: | |sinopsis=Racionaliza: | ||
| Línea 237: | Línea 237: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicios 2 | + | |titulo1=Ejercicio 2 |
| |duracion=8'53" | |duracion=8'53" | ||
| |sinopsis=Racionaliza: | |sinopsis=Racionaliza: | ||
| Línea 268: | Línea 268: | ||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Ejercicios 7 | + | |titulo1=Ejercicio 7 |
| |duracion=10'14" | |duracion=10'14" | ||
| |sinopsis=Racionaliza: | |sinopsis=Racionaliza: | ||
| Línea 275: | Línea 275: | ||
| |url1=https://www.youtube.com/watch?v=BrGBdNn6H7Q | |url1=https://www.youtube.com/watch?v=BrGBdNn6H7Q | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=9'34" | ||
| + | |sinopsis=Racionaliza: | ||
| + | |||
| + | a) <math>\cfrac{1}{\sqrt{2}}</math>{{b4}}{{b4}}b) <math>\cfrac{1}{\sqrt{x}}</math>{{b4}}{{b4}}c) <math>\cfrac{1}{\sqrt{5}+\sqrt{3}}</math>{{b4}}{{b4}} | ||
| + | d) <math>\cfrac{4}{\sqrt{6}-\sqrt{2}}</math>{{b4}}{{b4}}e) <math>\cfrac{1}{\sqrt[3]{2}}</math>{{b4}}{{b4}}f) <math>\cfrac{1}{\sqrt[4]{8}}</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=to1IBAQzjpE&index=42&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 10:05 13 jun 2017
Se llama racionalización al procedimiento por el cual a partir de una fracción con raíces en el denominador obtenemos otra fracción equivalente sin raíces en el denominador.
Los dos videotutoriales siguientes resumen lo que vamos a ver en este apartado:
Tutorial en el que se explica y trabaja la racionalización de quebrados con radicales, en el caso en que el denominador es un monomio, es decir, un único término.
- 00:00 a 02:50: Explicación del proceso de racionalización.
- 02:50 a 09:50: Ejemplos donde se analizan los errores más típicos cometidos en la racionalización con un monomio en el denominador.
- 09:50 a 17:18: Ejercicios de racionalización con monomios en el denominador.
Tutorial en el que se explica y trabaja la racionalización de quebrados con radicales, en el caso en que el denominador es un binomio, es decir, suma de dos términos.
- 00:00 a 01:30: Explicación del proceso de racionalización.
- 01:30 a 09:40: Ejemplo donde se analizan los errores más típicos cometidos en la racionalización con un binomio en el denominador.
- 09:40 a 13:35: Ejercicios de racionalización con binomios en el denominador.
- 13:35 a 17:14: Ejercicio de racionalización con un trinomio en el denominador.
Tabla de contenidos |
Caso 1: Denominador con raíces cuadradas
Procedimiento
Para racionalizar una fracción con una raíz cuadrada en el denominador se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma.
Ejemplo: Caso 1: Denominador con raíces cuadradas
Racionalizar 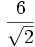
En este caso hay que multiplicar numerador y denominador por 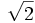
Caso 2: Denominador con otras raíces
Procedimiento
Para racionalizar una fracción con una raíz de índice distinto de dos en el denominador, se deben multiplicar el numerador y denominador de la fracción por una raíz con el mismo índice en la que cada exponente de los factores del radicando se calculará como:
- La diferencia entre el índice del radical y el exponente actual, caso de que el índice sea mayor o igual que el exponente actual.
- La diferencia entre el exponente actual y el múltiplo del indice más cercano a dicho exponente, caso de que el exponente actual supere al índice.
Ejemplo: Caso 2: Denominador con otras raíces
Racionalizar ![\frac{{2}}{\sqrt[5]{a^3b^4}}](/wikipedia/images/math/5/3/3/533185378740f77c6d3da802a18e1fdd.png)
En este ejemplo, hay que multiplicar numerador y denominador por ![\sqrt[5] {a^2b}](/wikipedia/images/math/3/d/5/3d57844c30135fee650c9bcfd98d40d1.png) , ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz:
, ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz:
Caso 3: Denominador con sumas y restas de raíces cuadradas
Procedimiento
Para racionalizar fracciones en cuyo denominador aparezcan binomios con alguna raíz cuadrada, se multiplica y divide por la expresión conjugada del denominador, esto es, por la misma expresión en la que solo se le cambia el signo del segundo término del binomio.
Ejemplo: Caso 3: Denominador con sumas y restas de raíces
Racionalizar 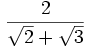
En este caso hay que multiplicar el numerador y el denominador por 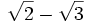 (este resultado es el que da el producto notable de los binomios conjugados):
(este resultado es el que da el producto notable de los binomios conjugados):
Racionaliza: 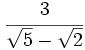 .
.
Racionaliza: 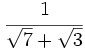 .
.
Racionaliza: 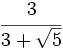 .
.
Racionaliza: 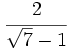 .
.
Racionaliza: 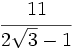 .
.
Racionaliza: 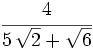 .
.
Racionaliza: 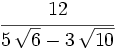 .
.
Racionaliza: 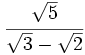 .
.
Racionaliza: 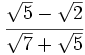 .
.
Caso 4: Denominador con sumas y restas de raíces cúbicas (Ampliación)
Para este caso deberás conocer primero las siguientes identidades de la suma y diferencia de cubos:
Demostración y ejemplos de las identidades:
- Suma de cubos:
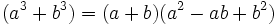
- Diferencia de cubos:
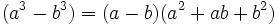
Actividades
Racionaliza:
a)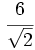 b)
b) ![\cfrac{6}{\sqrt[5]{2^2}}\;](/wikipedia/images/math/4/5/3/45300658ad66f636e45d5a937abb9ce2.png) c)
c) 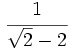 d)
d) 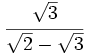
Racionaliza:
a)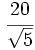 b)
b) ![\cfrac{16}{\sqrt[3]{2}}\;](/wikipedia/images/math/d/c/e/dce724def14d2562ee1fd77bf2833432.png) c)
c) ![\cfrac{22}{3\,\sqrt[5]{4}}\;](/wikipedia/images/math/2/b/0/2b086052936cad993cb0c4a22d48db74.png)
Racionaliza: ![\cfrac{3ab}{\sqrt[4]{a^2b^3c}}\;](/wikipedia/images/math/7/0/9/709ab631d1a8344d94c8314001dfa88f.png)
Racionaliza: 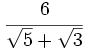
Simplifica: ![\cfrac{\sqrt[4]{a^3} \cdot a^{-1}}{a\,\sqrt{a}}\;](/wikipedia/images/math/d/c/4/dc4044e264b4425b4d26164a0f610b4d.png)
Racionaliza: 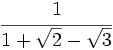
Racionaliza:
a) 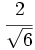 b)
b) ![\cfrac{4}{\sqrt[3]{5}}](/wikipedia/images/math/5/5/a/55ace2b51fb5fc69060e01f2b64ae22a.png) c)
c) ![\cfrac{3}{\sqrt[4]{729}}](/wikipedia/images/math/4/4/1/4414906695a164be992fb3ccd577a118.png) d)
d) ![\cfrac{5}{\sqrt[5]{125}}](/wikipedia/images/math/c/5/f/c5ffa5189009ca20a4f17a6a26380002.png)
Racionaliza:
a) 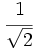 b)
b) 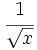 c)
c) 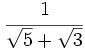 d)
d) 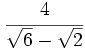 e)
e) ![\cfrac{1}{\sqrt[3]{2}}](/wikipedia/images/math/d/e/9/de9cd45023621984a57f028dd79d3f13.png) f)
f) ![\cfrac{1}{\sqrt[4]{8}}](/wikipedia/images/math/3/c/7/3c78c7350c28bda84045acdb35b5491a.png)
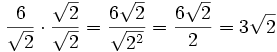
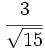 .
.
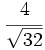 .
.
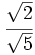 .
.
![\frac{{2}}{\sqrt[5]{a^3b^4}} \cdot \frac{\sqrt[5] {a^2b} }{\sqrt[5]{a^2b}} = \frac{{2\sqrt[5]{a^2b}}}{\sqrt[5]{a^5b^5}} = \frac{{2\sqrt[5]{a^2b}}}{{ab}}](/wikipedia/images/math/0/a/6/0a6d73fa5ee1fe441c50539e138ae167.png)
![\cfrac{2}{\sqrt[4]{3}}](/wikipedia/images/math/3/6/3/363cdd6889755a849dc9a7ea0bac576d.png) .
.
![\cfrac{1}{\sqrt[5]{8}}](/wikipedia/images/math/b/a/0/ba08551ff4220087d9fbb68dee2ffd73.png) .
.
![\cfrac{5}{2\,\sqrt[3]{7}}](/wikipedia/images/math/8/3/b/83b21b3caaf20fd75d0e6b3f0a3cc8c3.png) .
.
![\cfrac{4}{\sqrt[5]{72}}](/wikipedia/images/math/6/b/b/6bb931ba83b1b6b45859a0561fd025ca.png) .
.
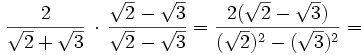
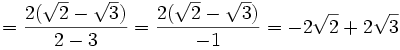
![\cfrac{1}{\sqrt[3]{9}+\sqrt[3]{2}}](/wikipedia/images/math/5/2/5/525844969b81af2a18046b55c583cf16.png) .
.
![\cfrac{2}{\sqrt[3]{7}-\sqrt[3]{3}}](/wikipedia/images/math/2/5/b/25b5b6bd40a7dd60bcdc8736b47d38e9.png) .
.
![\cfrac{2}{\sqrt[3]{25}+\sqrt[3]{15}+\sqrt[3]{9}}](/wikipedia/images/math/8/6/3/863071bfa12d745b2ba15899c0fb3793.png) .
.
![\cfrac{22}{\sqrt[3]{25}-\sqrt[3]{5}+1}](/wikipedia/images/math/c/e/1/ce1cad8992e279a2b317175de6241c79.png) .
.