Plantilla:Videos: Distancia entre dos puntos del plano
De Wikipedia
| Revisión de 11:06 18 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:09 18 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 21: | Línea 21: | ||
| }} | }} | ||
| ---- | ---- | ||
| + | Cálculo de distancias: | ||
| + | |||
| + | ---- | ||
| + | Halla la coordenada que falta: | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
Revisión de 11:09 18 jun 2017
- Módulo de un vector = distancia entre dos puntos. Demostración de la fórmula.
- Ejemplos y ejercicios.
Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
Cálculo de distancias:
Halla la coordenada que falta:
Halla el valor de "x" para que la distancia entre los puntos A(x,-1) y B(9,4) sea 13.
Halla el valor de "y" para que la distancia entre los puntos P(7,1) y Q(3,y) sea 5.
Halla el punto Q el eje Y que equidista de A(4,2) y B(5,5).
Halla el punto P el eje X que equidista de A(5,1) y B(0,6).
Halla el punto P que equidista de A(7,-3), B(8,-2) y C(0,-2).
La abscisa, x, de un punto P, es el doble de sus ordenada, y. P equidista de Q(4,-3) y R(1,6). Halla el punto P.
Polígonos:
Halla el perímetro del triángulo de vértices A(3,-8), B(-2,2) y C(7,-1).
Halla el perímetro del polígono de vértices A(3,2), B(5,5), C(-2,4) y D(-4,1).
Halla el área del triángulo de vértices P(-1,2), Q(2,4) y R(0,5), usando la fórmula de Herón.
Halla el área del triángulo de vértices P(6,0), Q(2,-5) y R(-2,-1), usando la fórmula de Herón.
Verifica que los puntos A(3,5), B(-1,-1) y C(4,4) son los vértices de un triángulo rectángulo. Halla su área.
Verifica que los puntos A(-2,4), B(6,2) y C(3,-1) son los vértices de un triángulo rectángulo. Halla su área.
Verifica que los puntos 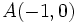 ,
, 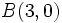 y
y 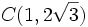 forman un triángulo equilátero.
forman un triángulo equilátero.
Verifica que los puntos A(-2,-3), B(-4,-5) y C(-1,-6) son los vértices de un triángulo isósceles.
Puntos colineales:
Determina si los puntos A(-3,1), B(0,2) y C(6,4) son colineales, usando distancias.
Determina si los puntos A(321), B(0,0) y C(9,6) son colineales, usando distancias.
Determina si los puntos A(-3,3), B(1,1/3) y C(3,-1) son colineales, usando distancias.

