Integral definida (2ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:10 18 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:39 27 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 54: | Línea 54: | ||
| |sinopsis=<math>\int_{1}^{2} \cfrac{x^4+2x^2-3x}{x^2} \, dx</math> | |sinopsis=<math>\int_{1}^{2} \cfrac{x^4+2x^2-3x}{x^2} \, dx</math> | ||
| }} | }} | ||
| + | }} | ||
| + | {{Videotutoriales|titulo=Integrales definidas|enunciado= | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=2'38" | ||
| + | |sinopsis=Calcula <math>\int_{\frac{1}{2}}^{1} \sqrt{1-x^2} \cdot dx</math> haciendo el cambio de variable <math>x= sen \, z</math>. | ||
| + | |||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/12-integrales-definidas/002-ejercicio-11 | ||
| }} | }} | ||
Revisión de 10:39 27 jun 2017
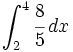
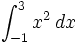
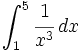
![\int_{-3}^{-1} \sqrt[3]{x^2} \, dx](/wikipedia/images/math/3/e/f/3ef78dfc1afd5490f8140c018cd83d2a.png)
![\int_{1}^{4} \sqrt[3]{27t} \, dt](/wikipedia/images/math/6/4/a/64af5171106055e85891eaee3fbc4713.png)
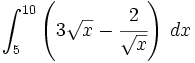
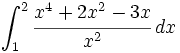
{{Videotutoriales|titulo=Integrales definidas|enunciado=
Calcula 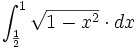 haciendo el cambio de variable
haciendo el cambio de variable 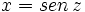 .
.

