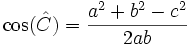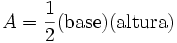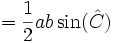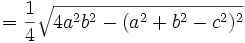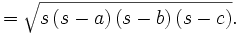Plantilla:Area triangulo
De Wikipedia
| Revisión de 10:11 29 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:11 29 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 25: | Línea 25: | ||
| |url1=https://www.youtube.com/watch?v=hIxbhfN9YNQ&list=PLWRbPOo5oaTePzUdB4MEeeKLuUgoKuN4M&index=3 | |url1=https://www.youtube.com/watch?v=hIxbhfN9YNQ&list=PLWRbPOo5oaTePzUdB4MEeeKLuUgoKuN4M&index=3 | ||
| }} | }} | ||
| - | {{Video_enlace_tutomate | + | {{Video_enlace |
| |titulo1=Área del triángulo (demostración) | |titulo1=Área del triángulo (demostración) | ||
| |duracion=3'26" | |duracion=3'26" | ||
Revisión de 10:11 29 jul 2017
|
|
Videotutorial que condensa todo lo que vamos a ver sobre medidas en los triángulos.
Demostración de área del triángulo.
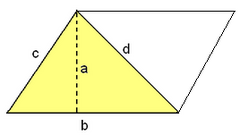
En esta escena podrás deducir la fórmula del área del triángulo.
Fórmula de Herón
Nota: El nivel de esta demostración corresponde a 1º de Bachillerato.
Una demostración moderna, que emplea álgebra y trigonometría (bastante distinta a la que dio Herón en su libro), podría ser la siguiente.
Supongamos un triángulo de lados  ,
, 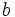 ,
, 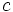 , cuyos ángulos opuestos a cada uno de esos lados son
, cuyos ángulos opuestos a cada uno de esos lados son 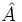 ,
, 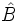 ,
, 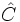 .
.
Por el teorema del coseno, tenemos que:
Por la relación fundamental de la trigonometría, tenemos que:
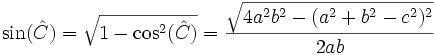 .
.
La altura de un triángulo de base  tiene una longitud
tiene una longitud 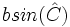 , por tanto siguiendo con la demostración
, por tanto siguiendo con la demostración
En esta escena podrás calcular el área de un triángulo mediante la fórmula de Herón.
Determinar el área y el perímetro de un triángulo cuyos lados miden 3, 4 y 5.
Determinar el área y el perímetro de un triángulo cuyos lados miden 4.4, 6.7 y 9.3.
Determinar el área y el perímetro de un triángulo rectángulo cuyos catetos miden 24 cm y 7 cm.
|
Actividad: El triángulo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
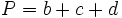
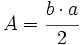
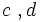 : lados.
: lados.
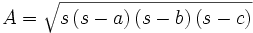
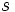 es el semiperímetro:
es el semiperímetro: 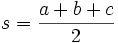 .
.