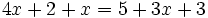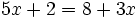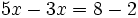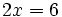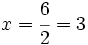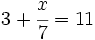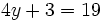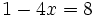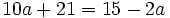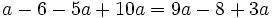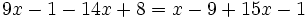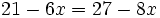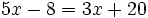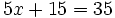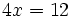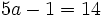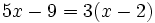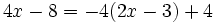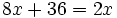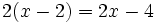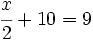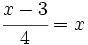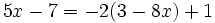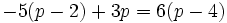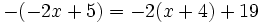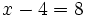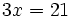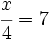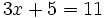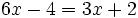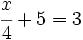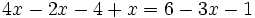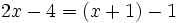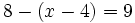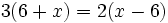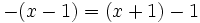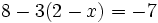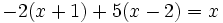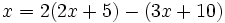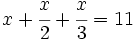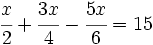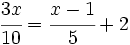Plantilla:Resolución de ecuaciones en casos más generales

De Wikipedia

(Diferencia entre revisiones)
Revisión de 17:34 11 sep 2017
Coordinador (Discusión | contribuciones)

← Ir a diferencia anterior		 Revisión de 17:57 11 sep 2017
Coordinador (Discusión | contribuciones)

Ir a siguiente diferencia →
Línea 25: Línea 25:
<center><math>x=\cfrac{6}{2}=3</math></center> <center><math>x=\cfrac{6}{2}=3</math></center>
 +}}
 +{{AI_cidead
 +|titulo1=Actividades: ''Resolución de ecuaciones''
 +|descripcion=Actividades en la que aprenderás y practicarás la resolución de ecuaciones de primer grado.
 +|url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena7/1quincena7_contenidos_3c.htm
 +}}
 +{{AI_cidead
 +|titulo1=Ejercicios: ''Resolución de ecuaciones''
 +|descripcion=Practica la resolución de ecuaciones de primer grado.
 +|url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena7/1quincena7_ejercicios_1c.htm
 +}}
 +{{p}}
 +{{Ejemplo_simple|titulo=Ejemplos: ''Ecuaciones de primer grado sencillas''|contenido=
 +Pulsa el botón EJEMPLO para ver más ecuaciones.
 +
 +<center><iframe>
 +url=http://maralboran.org/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_sfp_ej.html
 +width=700
 +height=230
 +name=myframe
 +</iframe></center>
 +<center>[http://maralboran.org/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_sfp_ej.html '''Click''' aquí si no se ve bien la escena]</center>
 +}}
 +{{p}}
 +{{Videotutoriales|titulo=Ejemplos: ''Ecuaciones de primer grado sencillas''|enunciado=
 +{{Video_enlace_virtual
 +|titulo1=Ejemplo 1
 +|duracion=2'40"
 +|sinopsis=Resuelve: <math>3+\cfrac{x}{7}=11\;</math>
 +|url1=https://www.youtube.com/watch?v=gqOdisXIC08&list=PLo7_lpX1yruOOLULOpmEnea_XS-EpZTtj&index=6
 +}}
 +{{Video_enlace_virtual
 +|titulo1=Ejemplo 2
 +|duracion=2'50"
 +|sinopsis=Resuelve: <math>4y+3=19\;</math>
 +|url1=https://www.youtube.com/watch?v=bw2GUJgF_p0&list=PLo7_lpX1yruOOLULOpmEnea_XS-EpZTtj&index=7
 +}}
 +{{Video_enlace_virtual
 +|titulo1=Ejemplo 3
 +|duracion=3'09"
 +|sinopsis=Resuelve: <math>1-4x=8\;</math>
 +|url1=https://www.youtube.com/watch?v=SMXM7MZpXsU&index=8&list=PLo7_lpX1yruOOLULOpmEnea_XS-EpZTtj
 +}}
 +{{Video_enlace_virtual
 +|titulo1=Ejemplo 4
 +|duracion=4'33"
 +|sinopsis=Resuelve: <math>10a+21=15-2a\;</math>
 +|url1=https://www.youtube.com/watch?v=Yvm_mSBzLGE&index=9&list=PLo7_lpX1yruOOLULOpmEnea_XS-EpZTtj
 +}}
 +{{Video_enlace_virtual
 +|titulo1=Ejemplo 5
 +|duracion=4'53"
 +|sinopsis=Resuelve: <math>a-6-5a+10a=9a-8+3a\;</math>
 +|url1=https://www.youtube.com/watch?v=7IsLDW8xRa8&list=PLo7_lpX1yruOOLULOpmEnea_XS-EpZTtj&index=10
 +}}
 +{{Video_enlace_virtual
 +|titulo1=Ejemplo 6
 +|duracion=4'55"
 +|sinopsis=Resuelve: <math>9x-1-14x+8=x-9+15x-1\;</math>
 +|url1=https://www.youtube.com/watch?v=bx8Rn802UiY&list=PLo7_lpX1yruOOLULOpmEnea_XS-EpZTtj&index=11
 +}}
 +{{Video_enlace_virtual
 +|titulo1=Ejemplo 7
 +|duracion=2'20"
 +|sinopsis=Resuelve: <math>21-6x=27-8x\;</math>
 +|url1=https://www.youtube.com/watch?v=HFf7_X0hSEk&index=12&list=PLo7_lpX1yruOOLULOpmEnea_XS-EpZTtj
 +}}
 +}}
 +{{p}}
 +{{Teorema_sin_demo|titulo=Procedimiento: Casos con paréntesis y denominadoes|enunciado=
 +*En el caso de tener paréntesis, éstos se efectuarán en primer lugar.
 +*En el caso de que algunos de los términos tengan denominador, todos los términos de la ecuación se multiplicarán por el m.c.m. de dichos denominadores.
 +}}
 +{{p}}
 +{{Ejemplo_simple|titulo=Ejemplos: ''Ecuaciones de primer grado con paréntesis''|contenido=
 +Pulsa el botón EJEMPLO para ver más ecuaciones.
 +
 +<center><iframe>
 +url=http://maralboran.org/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_p_ej.html
 +width=700
 +height=260
 +name=myframe
 +</iframe></center>
 +<center>[http://maralboran.org/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_p_ej.html '''Click''' aquí si no se ve bien la escena]</center>
 +}}
 +{{p}}
 +
 +{{Ejemplo_simple|titulo=Ejemplos: ''Ecuaciones de primer grado con denominadores''|contenido=
 +Pulsa el botón EJEMPLO para ver más ecuaciones.
 +
 +<center><iframe>
 +url=http://maralboran.org/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_f_ej.html
 +width=700
 +height=260
 +name=myframe
 +</iframe></center>
 +<center>[http://maralboran.org/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_f_ej.html '''Click''' aquí si no se ve bien la escena]</center>
 +}}
 +{{p}}
 +{{Videotutoriales|titulo=Resolución de ecuaciones de primer grado con una incógnita|enunciado=
 +{{Video_enlace_tutomate
 +|titulo1=Ecuaciones sin paréntesis
 +|duracion=9'00"
 +|sinopsis=Ejemplos de resolución de ecuaciones de primer grado sencillas y más generales.
 +|url1=https://www.youtube.com/watch?v=nrhq1pBoby0&index=4&list=PLWRbPOo5oaTcOfNT053lPqygv7Wx5PIwY
 +}}
 +{{Video_enlace_tutomate
 +|titulo1=Ecuaciones con paréntesis
 +|duracion=9'27"
 +|sinopsis=Ejemplos de resolución de ecuaciones de primer grado con paréntesis.
 +|url1=https://www.youtube.com/watch?v=H7lR7KkSM7Y&list=PLWRbPOo5oaTcOfNT053lPqygv7Wx5PIwY&index=5
 +}}
 +{{Video_enlace_tutomate
 +|titulo1=Ecuaciones con denominadores
 +|duracion=8'19"
 +|sinopsis=Ejemplos de resolución de ecuaciones de primer grado con denominadores.
 +|url1=https://www.youtube.com/watch?v=to27Vpf8WRo&list=PLWRbPOo5oaTcOfNT053lPqygv7Wx5PIwY&index=6
 +}}
 +{{Video_enlace_tutomate
 +|titulo1=Ecuaciones con paréntesis y denominadores
 +|duracion=9'04"
 +|sinopsis=Ejemplos de resolución de ecuaciones de primer grado con denominadores.
 +|url1=https://www.youtube.com/watch?v=nZ9NjJU2P2c&index=7&list=PLWRbPOo5oaTcOfNT053lPqygv7Wx5PIwY
 +}}
 +----
 +{{Tabla50|celda1=
 +{{Video_enlace_paps
 +|titulo1=Ejercicio 1
 +|duracion=3'29"
 +|sinopsis=Resuelve:
 +
 +a) <math>5x-8=3x+20\;</math>
 +
 +b) <math>5x+15=35\;</math>
 +
 +c) <math>4x=12\;</math>|url1=https://www.youtube.com/watch?v=LxLlSyKykM4
 +}}
 +{{Video_enlace_julioprofe
 +|titulo1=Ejercicio 2
 +|duracion=5'13"
 +|sinopsis=Resuelve:
 +
 +a) <math>5a-1=14\;</math>
 +
 +b) <math>5x-9=3(x-2)\;</math>
 +
 +c) <math>4x-8=-4(2x-3)+4\;</math>
 +|url1=https://www.youtube.com/watch?v=qeKEA066OSs&list=PL9B9AC3136D2D4C45&index=26
 +}}
 +{{Video_enlace_unicoos
 +|titulo1=Ejercicio 3
 +|duracion=11'44"
 +|sinopsis=Resuelve:
 +
 +a) <math>8x+36=2x\;</math>
 +
 +b) <math>2(x-2)=2x-4\;</math>
 +
 +c) <math>3x+2=3x\;</math>
 +
 +d) <math>\cfrac{x}{2}+10=9\;</math>
 +
 +e) <math>\cfrac{x-3}{4}=x\;</math>
 +|url1=http://www.unicoos.com/video/matematicas/1-eso/expresiones-algebraicas/ecuaciones-de-primer-grado/ecuaciones-de-primer-grado-01
 +}}
 +{{Video_enlace_julioprofe
 +|titulo1=Ejercicio 4
 +|duracion=2'48"
 +|sinopsis=Resuelve la ecuación: <math>5x-7=-2(3-8x)+1\;</math>
 +|url1=https://www.youtube.com/watch?v=xeUWLZY4roM&list=PL9B9AC3136D2D4C45&index=27
 +}}
 +{{Video_enlace_julioprofe
 +|titulo1=Ejercicio 5
 +|duracion=2'42"
 +|sinopsis=Resuelve la ecuación: <math>-5(p-2)+3p=6(p-4)\;</math>
 +|url1=https://www.youtube.com/watch?v=LD2VeoX0J4A&list=PL9B9AC3136D2D4C45&index=28
 +}}
 +|celda2=
 +{{Video_enlace_julioprofe
 +|titulo1=Ejercicio 6
 +|duracion=3'15"
 +|sinopsis=Resuelve la ecuación: <math>-(-2x+5)=-2(x+4)+19\;</math>
 +|url1=https://www.youtube.com/watch?v=h4gt8tsVJbw&list=PL9B9AC3136D2D4C45&index=29
 +}}
 +{{Video_enlace_clasematicas
 +|titulo1=Ejercicio 7
 +|duracion=17'34"
 +|sinopsis=Resuelve:
 +
 +a) <math>x-4=8\;</math>
 +
 +b) <math>3x=21\;</math>
 +
 +c) <math>\cfrac{x}{4}=7\;</math>
 +
 +d) <math>3x+5=11\;</math>
 +
 +e) <math>6x-4=3x+2\;</math>
 +
 +f) <math>\cfrac{x}{4}+5=3\;</math>
 +
 +g) <math>4x-2x-4+x=6-3x-1\;</math>
 +
 +h) <math>2x-4=(x+1)-1\;</math>
 +
 +i) <math>8-(x-4)=9\;</math>
 +
 +|url1=https://www.youtube.com/watch?v=sa-wcWIkz8o&index=1&list=PLZNmE9BEzVImQnTPBs51x5IR2UdM3SHF1
 +}}
 +{{Video_enlace_clasematicas
 +|titulo1=Ejercicio 8
 +|duracion=11'05"
 +|sinopsis=Resuelve:
 +
 +a) <math>3(6+x)=2(x-6)\;</math>
 +
 +b) <math>-(x-1)=(x+1)-1\;</math>
 +
 +c) <math>8-3(2-x)=-7\;</math>
 +
 +|url1=https://www.youtube.com/watch?v=71qcp9DpzP0&index=2&list=PLZNmE9BEzVImQnTPBs51x5IR2UdM3SHF1
 +}}
 +{{Video_enlace_clasematicas
 +|titulo1=Ejercicio 9
 +|duracion=9'20"
 +|sinopsis=Resuelve:
 +
 +a) <math>-2(x+1)+5(x-2)=x\;</math>
 +
 +b) <math>x=2(2x+5)-(3x+10)\;</math>
 +
 +c) <math>2(x+1)-3(x-2)=x+6\;</math>
 +
 +|url1=https://www.youtube.com/watch?v=lE73xT6a8WQ&list=PLZNmE9BEzVImQnTPBs51x5IR2UdM3SHF1&index=3
 +}}
 +{{Video_enlace_clasematicas
 +|titulo1=Ejercicio 10
 +|duracion=8'18"
 +|sinopsis=Resuelve:
 +
 +a) <math>x+\cfrac{x}{2}+\cfrac{x}{3}=11\;</math>
 +
 +b) <math>\cfrac{x}{2}+\cfrac{3x}{4}-\cfrac{5x}{6}=15\;</math>
 +
 +c) <math>\cfrac{3x}{10}=\cfrac{x-1}{5}+2\;</math>
 +
 +|url1=https://www.youtube.com/watch?v=1rbwzgyFx20&list=PLZNmE9BEzVImQnTPBs51x5IR2UdM3SHF1&index=4
 +}}
 +}}
 +}}
 +{{p}}
 +
 +{{AI_anaya|titulo1=Autoevaluación 1: ''Resolución de ecuaciones''
 +|descripcion=
 +
 +<center><iframe>
 +url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/10/06.htm
 +width=800
 +height=650
 +name=myframe
 +</iframe></center>
 +
 +|url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/10/06.htm
}} }}

Revisión de 17:57 11 sep 2017

ejercicio

Procedimiento

Para resolver ecuaciones de primer grado con una incógnita transformaremos la ecuación de partida en otra equivalente, más sencilla, por medio de los siguientes recursos:

  • Reduciendo sus miembros, es decir, agrupando términos semejantes.
  • Trasponiendo términos, esto es, utilizando las técnicas para casos sencillos vistas en los apartados anteriores.

ejercicio
Ejemplo

Resolvamos la siguiente ecuación:

4x+2+x=5+3x+3\;

Reducimos:

5x+2=8+3x\;

Trasponemos:

5x-3x=8-2\;

Reducimos:

2x=6\;

Trasponemos:

x=\cfrac{6}{2}=3
Actividades: Resolución de ecuaciones     Descripción:

Actividades en la que aprenderás y practicarás la resolución de ecuaciones de primer grado.

Ejercicios: Resolución de ecuaciones     Descripción:

Practica la resolución de ecuaciones de primer grado.

ejercicio
Ejemplos: Ecuaciones de primer grado sencillas

Pulsa el botón EJEMPLO para ver más ecuaciones.

Click aquí si no se ve bien la escena

video
Ejemplos: Ecuaciones de primer grado sencillas
Ejemplo 1 (2'40")     Sinopsis:

Resuelve: 3+\cfrac{x}{7}=11\;

Ejemplo 2 (2'50")     Sinopsis:

Resuelve: 4y+3=19\;

Ejemplo 3 (3'09")     Sinopsis:

Resuelve: 1-4x=8\;

Ejemplo 4 (4'33")     Sinopsis:

Resuelve: 10a+21=15-2a\;

Ejemplo 5 (4'53")     Sinopsis:

Resuelve: a-6-5a+10a=9a-8+3a\;

Ejemplo 6 (4'55")     Sinopsis:

Resuelve: 9x-1-14x+8=x-9+15x-1\;

Ejemplo 7 (2'20")     Sinopsis:

Resuelve: 21-6x=27-8x\;

ejercicio

Procedimiento: Casos con paréntesis y denominadoes

  • En el caso de tener paréntesis, éstos se efectuarán en primer lugar.
  • En el caso de que algunos de los términos tengan denominador, todos los términos de la ecuación se multiplicarán por el m.c.m. de dichos denominadores.

ejercicio
Ejemplos: Ecuaciones de primer grado con paréntesis

Pulsa el botón EJEMPLO para ver más ecuaciones.

Click aquí si no se ve bien la escena

ejercicio
Ejemplos: Ecuaciones de primer grado con denominadores

Pulsa el botón EJEMPLO para ver más ecuaciones.

Click aquí si no se ve bien la escena

video
Resolución de ecuaciones de primer grado con una incógnita
Ecuaciones sin paréntesis (9'00")     Sinopsis:

Ejemplos de resolución de ecuaciones de primer grado sencillas y más generales.

Ecuaciones con paréntesis (9'27")     Sinopsis:

Ejemplos de resolución de ecuaciones de primer grado con paréntesis.

Ecuaciones con denominadores (8'19")     Sinopsis:

Ejemplos de resolución de ecuaciones de primer grado con denominadores.

Ecuaciones con paréntesis y denominadores (9'04")     Sinopsis:

Ejemplos de resolución de ecuaciones de primer grado con denominadores.

Ejercicio 1 (3'29")     Sinopsis:

Resuelve:

a) 5x-8=3x+20\;

b) 5x+15=35\;

c) 4x=12\;

Ejercicio 2 (5'13")     Sinopsis:

Resuelve:

a) 5a-1=14\;

b) 5x-9=3(x-2)\;

c) 4x-8=-4(2x-3)+4\;

Ejercicio 3 (11'44")     Sinopsis:

Resuelve:

a) 8x+36=2x\;

b) 2(x-2)=2x-4\;

c) 3x+2=3x\;

d) \cfrac{x}{2}+10=9\;

e) \cfrac{x-3}{4}=x\;

Ejercicio 4 (2'48")     Sinopsis:

Resuelve la ecuación: 5x-7=-2(3-8x)+1\;

Ejercicio 5 (2'42")     Sinopsis:

Resuelve la ecuación: -5(p-2)+3p=6(p-4)\;

Ejercicio 6 (3'15")     Sinopsis:

Resuelve la ecuación: -(-2x+5)=-2(x+4)+19\;

Ejercicio 7 (17'34")     Sinopsis:

Resuelve:

a) x-4=8\;

b) 3x=21\;

c) \cfrac{x}{4}=7\;

d) 3x+5=11\;

e) 6x-4=3x+2\;

f) \cfrac{x}{4}+5=3\;

g) 4x-2x-4+x=6-3x-1\;

h) 2x-4=(x+1)-1\;

i) 8-(x-4)=9\;

Ejercicio 8 (11'05")     Sinopsis:

Resuelve:

a) 3(6+x)=2(x-6)\;

b) -(x-1)=(x+1)-1\;

c) 8-3(2-x)=-7\;

Ejercicio 9 (9'20")     Sinopsis:

Resuelve:

a) -2(x+1)+5(x-2)=x\;

b) x=2(2x+5)-(3x+10)\;

c) 2(x+1)-3(x-2)=x+6\;

Ejercicio 10 (8'18")     Sinopsis:

Resuelve:

a) x+\cfrac{x}{2}+\cfrac{x}{3}=11\;

b) \cfrac{x}{2}+\cfrac{3x}{4}-\cfrac{5x}{6}=15\;

c) \cfrac{3x}{10}=\cfrac{x-1}{5}+2\;

Autoevaluación 1: Resolución de ecuaciones     Descripción:
Obtenido de "http://www.maralboran.org/wikipedia/index.php/Plantilla:Resoluci%C3%B3n_de_ecuaciones_en_casos_m%C3%A1s_generales"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda