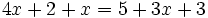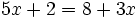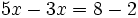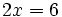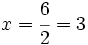Plantilla:Resolución de ecuaciones en casos más generales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:25 11 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:27 11 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 50: | Línea 50: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Ejemplos: ''Ecuaciones de primer grado''|enunciado= | + | {{Videotutoriales|titulo=Ejercicios: ''Ecuaciones de primer grado''|enunciado= |
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejemplo 1 | + | |titulo1=Ejercicio 1 |
| |duracion=2'40" | |duracion=2'40" | ||
| |sinopsis=Resuelve: <math>3+\cfrac{x}{7}=11\;</math> | |sinopsis=Resuelve: <math>3+\cfrac{x}{7}=11\;</math> | ||
| Línea 58: | Línea 58: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejemplo 2 | + | |titulo1=Ejercicio 2 |
| |duracion=2'50" | |duracion=2'50" | ||
| |sinopsis=Resuelve: <math>4y+3=19\;</math> | |sinopsis=Resuelve: <math>4y+3=19\;</math> | ||
| Línea 64: | Línea 64: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejemplo 3 | + | |titulo1=Ejercicio 3 |
| |duracion=3'09" | |duracion=3'09" | ||
| |sinopsis=Resuelve: <math>1-4x=8\;</math> | |sinopsis=Resuelve: <math>1-4x=8\;</math> | ||
| Línea 70: | Línea 70: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejemplo 4 | + | |titulo1=Ejercicio 4 |
| |duracion=4'33" | |duracion=4'33" | ||
| |sinopsis=Resuelve: <math>10a+21=15-2a\;</math> | |sinopsis=Resuelve: <math>10a+21=15-2a\;</math> | ||
| Línea 76: | Línea 76: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejemplo 5 | + | |titulo1=Ejercicio 5 |
| |duracion=4'53" | |duracion=4'53" | ||
| |sinopsis=Resuelve: <math>a-6-5a+10a=9a-8+3a\;</math> | |sinopsis=Resuelve: <math>a-6-5a+10a=9a-8+3a\;</math> | ||
| Línea 82: | Línea 82: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejemplo 6 | + | |titulo1=Ejercicio 6 |
| |duracion=4'55" | |duracion=4'55" | ||
| |sinopsis=Resuelve: <math>9x-1-14x+8=x-9+15x-1\;</math> | |sinopsis=Resuelve: <math>9x-1-14x+8=x-9+15x-1\;</math> | ||
| Línea 88: | Línea 88: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Ejemplo 7 | + | |titulo1=Ejercicio 7 |
| |duracion=2'20" | |duracion=2'20" | ||
| |sinopsis=Resuelve: <math>21-6x=27-8x\;</math> | |sinopsis=Resuelve: <math>21-6x=27-8x\;</math> | ||
Revisión de 18:27 11 sep 2017
Procedimiento
Para resolver ecuaciones de primer grado con una incógnita transformaremos la ecuación de partida en otra equivalente, más sencilla, por medio de los siguientes recursos:
- Reduciendo sus miembros, es decir, agrupando términos semejantes.
- Trasponiendo términos, esto es, utilizando las técnicas para casos sencillos vistas en los apartados anteriores.
Resolvamos la siguiente ecuación:
Reducimos:
Trasponemos:
Reducimos:
Trasponemos:
Actividades: Resolución de ecuaciones Descripción: Actividades en la que aprenderás y practicarás la resolución de ecuaciones de primer grado.
Ejercicios: Resolución de ecuaciones Descripción: Practica la resolución de ecuaciones de primer grado.
Ejercicio 1 (2'40") Sinopsis: Resuelve: 
Ejercicio 2 (2'50") Sinopsis: Resuelve: 
Ejercicio 3 (3'09") Sinopsis: Resuelve: 
Ejercicio 4 (4'33") Sinopsis: Resuelve: 
Ejercicio 5 (4'53") Sinopsis: Resuelve: 
Ejercicio 6 (4'55") Sinopsis: Resuelve: 
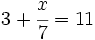
Ejercicio 7 (2'20") Sinopsis: 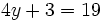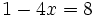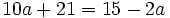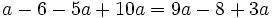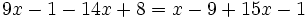Resuelve: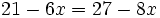 
Resolución de ecuaciones con paréntesis y/o denominadores
Procedimiento
- En el caso de que la ecuación presente paréntesis, éstos se efectuarán en primer lugar.
- En el caso de que algunos de los términos de la ecuación tengan denominador, todos los términos de la ecuación se multiplicarán por el m.c.m. de dichos denominadores.
