Sistemas de ecuaciones lineales (2º ESO)

De Wikipedia

(Diferencia entre revisiones)

Coordinador (Discusión | contribuciones)

Ir a siguiente diferencia →

Revisión de 16:38 14 sep 2017

Menú:
Enlaces internos Para repasar Para ampliar Enlaces externos
Indice
Descartes
Manual Casio
 WIRIS
Calculadora

Tabla de contenidos

[editar]

Introducción

Los siguientes videotutoriales resumen gran parte de los conceptos que vamos a ver en esta página:

Ecuaciones y sistemas. Definiciones básicas (15´53")     Sinopsis:

Tutorial en el que se dan los conceptos básicos respecto a las ecuaciones y sistemas de ecuaciones.

  • 00:00 a 01:40: Definición de expresión algebraica.
  • 01:40 a 04:00: Definición y ejemplos de ecuaciones.
  • 04:00 a 08:32: Definición y ejemplo de solución de una ecuación.
  • 08:32 a 10:02: Definición de tipos de igualdades según sus soluciones.
  • 10:02 a 10:48: Definición y ejemplos de sistemas de ecuaciones.
  • 10:48 a 14:20: Definición y ejemplo de solución de un sistema de ecuaciones.
  • 14:20 a Fin: Definición de tipos de sistema de ecuaciones según sus soluciones.

Sistemas de dos ecuaciones lineales con dos incógnitas (11´07")     Sinopsis:

Interpretación geométrica de los sistemas lineales de 2 ecuaciones con 2 incógnitas (9´33")     Sinopsis:

Videotutorial

(Pág. 162)

[editar]

Sistemas de ecuaciones lineales 2x2

  • Un sistema de dos ecuaciones de primer grado con dos incógnitas o simplemente, sistema 2x2 de ecuaciones lineales, es la agrupación de dos ecuaciones de primer grado con dos incógnitas:
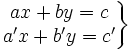
\left . \begin{matrix} ax+by=c \\ a'x+b'y=c'\end{matrix} \right \}
  • Se llama solución de un sistema 2x2, a cualquier pareja de valores 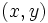(x,y)\; que sea solución de ambas ecuaciones a la vez. Las soluciones de este tipo de sistemas son los puntos de corte de las rectas que representan cada una de las ecuaciones del sistema.

ejercicio

Ejemplo: Solución de un sistema de ecuaciones

Comprueba si las parejas de números (1,2) y (-1,3) son o no soluciones del sistema:

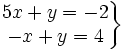
\left . \begin{matrix} 5x+y=-2 \\ -x+y=4 \end{matrix} \right \}
Solución:
  • Para comprobar si (1,2) es solución, sustituimos x=1 e y=2 en las dos ecuaciones del sistema:
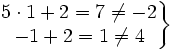
\left . \begin{matrix} 5 \cdot 1+ 2=7 \ne -2 \\ -1+2=1 \ne 4 \end{matrix} \right \}

Como no se verifican las dos ecuaciones, la pareja (1,2) no es solución del sistema.

  • Para comprobar si (-1,3) es solución, sustituimos x=-1 e y=3 en las dos ecuaciones del sistema:
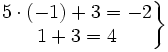
\left . \begin{matrix} 5 \cdot (-1)+ 3=-2 \\ 1+3= 4 \end{matrix} \right \}
Ahora si se verifican las dos ecuaciones, por tanto, la pareja (-1,3) si es solución del sistema.

video
Sistemas de ecuaciones lineales 2x2. Soluciones
Tutorial (1´00")     Sinopsis:
  • Ecuación lineal con dos incógnitas. Soluciones.
  • Sistema de ecuaciones lineales con dos incógnitas. Soluciones.
Ejercicio (4´26")     Sinopsis:

Comprueba si el par (-1,7) es solución del siguiente sistema:

\left . \begin{matrix} ~~x+2y &=~~13 \\ 3x-~y &=-11 \end{matrix} \right \}

video
Sistema de ecuaciones lineales 2x2. Soluciones
Autoevaluación 1     Descripción:

Ejercicios de autoevaluación sobre sistemas de ecuaciones lineales.

Autoevaluación 2     Descripción:

Comprueba soluciones de sistemas de ecuaciones lineales.

[editar]

Ejercicios propuestos

ejercicio

Ejercicios propuestos: Sistemas de ecuaciones lineales

(Pág. 162)

1a; 2b

1b; 2a

Obtenido de "http://www.maralboran.org/wikipedia/index.php/Sistemas_de_ecuaciones_lineales_%282%C2%BA_ESO%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda