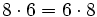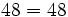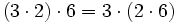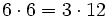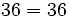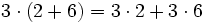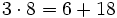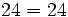Plantilla:Propiedades de la multiplicación de números naturales
De Wikipedia
| Revisión de 18:48 2 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:58 14 sep 2018 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 48: | Línea 48: | ||
| |duracion=3'17" | |duracion=3'17" | ||
| |sinopsis=Propiedades conmutativa y asociativa del producto de números naturales. Ejemplos. | |sinopsis=Propiedades conmutativa y asociativa del producto de números naturales. Ejemplos. | ||
| - | |url1=https://www.youtube.com/watch?v=RDyeZCWbO-I&list=PLTDunuLIi6ogbD4_joialQfNyKekQcbnG&index=6 | + | |url1=http://www.youtube.com/watch?v=RDyeZCWbO-I&list=PLTDunuLIi6ogbD4_joialQfNyKekQcbnG&index=6 |
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| Línea 54: | Línea 54: | ||
| |duracion=3'20" | |duracion=3'20" | ||
| |sinopsis=Propiedad distributiva de los números naturales. Ejemplos. | |sinopsis=Propiedad distributiva de los números naturales. Ejemplos. | ||
| - | |url1=https://www.youtube.com/watch?v=z-fEdNUMyvw&index=7&list=PLTDunuLIi6ogbD4_joialQfNyKekQcbnG | + | |url1=http://www.youtube.com/watch?v=z-fEdNUMyvw&index=7&list=PLTDunuLIi6ogbD4_joialQfNyKekQcbnG |
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| Línea 60: | Línea 60: | ||
| |duracion=3'04" | |duracion=3'04" | ||
| |sinopsis=El elemento neutro de la suma y del producto de números naturales. Ejemplos. | |sinopsis=El elemento neutro de la suma y del producto de números naturales. Ejemplos. | ||
| - | |url1=https://www.youtube.com/watch?v=NFWWecp3RjQ&list=PLTDunuLIi6ogbD4_joialQfNyKekQcbnG&index=8 | + | |url1=http://www.youtube.com/watch?v=NFWWecp3RjQ&list=PLTDunuLIi6ogbD4_joialQfNyKekQcbnG&index=8 |
| }} | }} | ||
| {{Video_enlace_tutomate | {{Video_enlace_tutomate | ||
| Línea 66: | Línea 66: | ||
| |duracion=7'08" | |duracion=7'08" | ||
| |sinopsis=Ejemplos de uso de la propiedad distributiva y de cómo se saca factor común. | |sinopsis=Ejemplos de uso de la propiedad distributiva y de cómo se saca factor común. | ||
| - | |url1=https://www.youtube.com/watch?v=ybM9xVjyK6Q&list=PLWRbPOo5oaTcIY1gMt5ILwioM6DTfpMk3&index=3 | + | |url1=http://www.youtube.com/watch?v=ybM9xVjyK6Q&list=PLWRbPOo5oaTcIY1gMt5ILwioM6DTfpMk3&index=3 |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 72: | Línea 72: | ||
| |duracion=8'40" | |duracion=8'40" | ||
| |sinopsis=Propiedad asociativa y conmutativa de forma visual. | |sinopsis=Propiedad asociativa y conmutativa de forma visual. | ||
| - | |url1=https://www.youtube.com/watch?v=8Z4vHn7tD2o | + | |url1=http://www.youtube.com/watch?v=8Z4vHn7tD2o |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 78: | Línea 78: | ||
| |duracion=11'39" | |duracion=11'39" | ||
| |sinopsis=Propiedad distributiva de forma visual. | |sinopsis=Propiedad distributiva de forma visual. | ||
| - | |url1=https://www.youtube.com/watch?v=OGvOZ2MeytI | + | |url1=http://www.youtube.com/watch?v=OGvOZ2MeytI |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 84: | Línea 84: | ||
| |duracion=8'40" | |duracion=8'40" | ||
| |sinopsis=Más formas de pensar en la multiplicación. Multiplicando usando la propiedad asociativa. | |sinopsis=Más formas de pensar en la multiplicación. Multiplicando usando la propiedad asociativa. | ||
| - | |url1=https://www.youtube.com/watch?v=99fQr49Zqqg | + | |url1=http://www.youtube.com/watch?v=99fQr49Zqqg |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 90: | Línea 90: | ||
| |duracion=6'25" | |duracion=6'25" | ||
| |sinopsis=Otra forma de multiplicar usando la propiedad distributiva. | |sinopsis=Otra forma de multiplicar usando la propiedad distributiva. | ||
| - | |url1=https://www.youtube.com/watch?v=wD22Eox9UVQ | + | |url1=http://www.youtube.com/watch?v=wD22Eox9UVQ |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 96: | Línea 96: | ||
| |duracion=1'36" | |duracion=1'36" | ||
| |sinopsis=El elemento neutro de la multiplicación de números naturales es el 1. | |sinopsis=El elemento neutro de la multiplicación de números naturales es el 1. | ||
| - | |url1=https://www.youtube.com/watch?v=HdkLiPeftRc | + | |url1=http://www.youtube.com/watch?v=HdkLiPeftRc |
| }} | }} | ||
| {{Video_enlace_mywhyu | {{Video_enlace_mywhyu | ||
| Línea 104: | Línea 104: | ||
| (Disponibles los subtítulos en inglés) | (Disponibles los subtítulos en inglés) | ||
| - | |url1=https://www.youtube.com/watch?v=rXXrzaDaETI&t=11s&index=6&list=PL7F6C8576EBEDD88F | + | |url1=http://www.youtube.com/watch?v=rXXrzaDaETI&t=11s&index=6&list=PL7F6C8576EBEDD88F |
| }} | }} | ||
| {{Video_enlace_mywhyu | {{Video_enlace_mywhyu | ||
| Línea 112: | Línea 112: | ||
| (Disponibles los subtítulos en inglés) | (Disponibles los subtítulos en inglés) | ||
| - | |url1=https://www.youtube.com/watch?v=CkVJ8xa63ow&t=1s&index=7&list=PL7F6C8576EBEDD88F | + | |url1=http://www.youtube.com/watch?v=CkVJ8xa63ow&t=1s&index=7&list=PL7F6C8576EBEDD88F |
| }} | }} | ||
| ---- | ---- | ||
| Línea 119: | Línea 119: | ||
| |duracion=4'02" | |duracion=4'02" | ||
| |sinopsis=Usa la propiedad conmutativa de la multiplicación para multiplicar 2 · 34 de diferente manera y comprueba que se obtienen los mismos resultados. | |sinopsis=Usa la propiedad conmutativa de la multiplicación para multiplicar 2 · 34 de diferente manera y comprueba que se obtienen los mismos resultados. | ||
| - | |url1=https://www.youtube.com/watch?v=tZSLBN_mVo0 | + | |url1=http://www.youtube.com/watch?v=tZSLBN_mVo0 |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 125: | Línea 125: | ||
| |duracion=2'47" | |duracion=2'47" | ||
| |sinopsis=Usa la propiedad asociativa de la multiplicación para multiplicar (12 · 3) · 10 de diferente manera y comprueba que se obtienen los mismos resultados. | |sinopsis=Usa la propiedad asociativa de la multiplicación para multiplicar (12 · 3) · 10 de diferente manera y comprueba que se obtienen los mismos resultados. | ||
| - | |url1=https://www.youtube.com/watch?v=D-zp1cf7AaI | + | |url1=http://www.youtube.com/watch?v=D-zp1cf7AaI |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 131: | Línea 131: | ||
| |duracion=2'36" | |duracion=2'36" | ||
| |sinopsis=Usa la propiedad distributiva de la multiplicación sobre la suma para calcular 4·(8 + 3). | |sinopsis=Usa la propiedad distributiva de la multiplicación sobre la suma para calcular 4·(8 + 3). | ||
| - | |url1=https://www.youtube.com/watch?v=OS2UhXETv8E | + | |url1=http://www.youtube.com/watch?v=OS2UhXETv8E |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 137: | Línea 137: | ||
| |duracion=1'48" | |duracion=1'48" | ||
| |sinopsis=Usa la propiedad distributiva de la multiplicación sobre la resta para calcular 5·(9 - 4). | |sinopsis=Usa la propiedad distributiva de la multiplicación sobre la resta para calcular 5·(9 - 4). | ||
| - | |url1=https://www.youtube.com/watch?v=QCPQFjdM-RU | + | |url1=http://www.youtube.com/watch?v=QCPQFjdM-RU |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 155: | Línea 155: | ||
| |duracion=4'02" | |duracion=4'02" | ||
| |sinopsis=Multiplica 6 · 7981 usando la propiedad distributiva. | |sinopsis=Multiplica 6 · 7981 usando la propiedad distributiva. | ||
| - | |url1=https://www.youtube.com/watch?v=fCB-FSUkEiw | + | |url1=http://www.youtube.com/watch?v=fCB-FSUkEiw |
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| Línea 161: | Línea 161: | ||
| |duracion=6'48" | |duracion=6'48" | ||
| |sinopsis=Multiplica 78 · 65 usando la propiedad distributiva. | |sinopsis=Multiplica 78 · 65 usando la propiedad distributiva. | ||
| - | |url1=https://www.youtube.com/watch?v=PLXRl0JKrMo | + | |url1=http://www.youtube.com/watch?v=PLXRl0JKrMo |
| }} | }} | ||
| }} | }} | ||
Revisión de 06:58 14 sep 2018
Propiedades de la multiplicación
- Operación interna: El producto de dos números naturales es otro número natural:
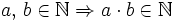
- Propiedad conmutativa: El producto no varía al cambiar el orden de los factores.
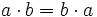
- Propiedad asociativa: El resultado de una multiplicación es independiente de la forma en que se agrupen los factores.

- Propiedad distributiva: El producto de un número por una suma (o resta) es igual a la suma (o resta) de los productos del número por cada sumando.

- Elemento neutro: El elemento neutro para la multiplicación es el 1.
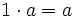
Propiedades conmutativa y asociativa del producto de números naturales. Ejemplos.
Propiedad distributiva de los números naturales. Ejemplos.
El elemento neutro de la suma y del producto de números naturales. Ejemplos.
Ejemplos de uso de la propiedad distributiva y de cómo se saca factor común.
Propiedad asociativa y conmutativa de forma visual.
Propiedad distributiva de forma visual.
Más formas de pensar en la multiplicación. Multiplicando usando la propiedad asociativa.
Otra forma de multiplicar usando la propiedad distributiva.
El elemento neutro de la multiplicación de números naturales es el 1.
The commutative property is common to the operations of both addition and multiplication and is an important property of many mathematical systems.
(Disponibles los subtítulos en inglés)
A look at the logic behind the associative and distributive properties of multiplication.
(Disponibles los subtítulos en inglés)
Usa la propiedad conmutativa de la multiplicación para multiplicar 2 · 34 de diferente manera y comprueba que se obtienen los mismos resultados.
Usa la propiedad asociativa de la multiplicación para multiplicar (12 · 3) · 10 de diferente manera y comprueba que se obtienen los mismos resultados.
Usa la propiedad distributiva de la multiplicación sobre la suma para calcular 4·(8 + 3).
Usa la propiedad distributiva de la multiplicación sobre la resta para calcular 5·(9 - 4).
Usa la propiedad distributiva de la multiplicación sobre la suma para sacar factor común en las siguientes expresiones:
- a) 20 + 30
- b) 90 + 27
- c) 55 + 35
- d) 12 + 75
Multiplica 6 · 7981 usando la propiedad distributiva.
Multiplica 78 · 65 usando la propiedad distributiva.
Propiedad conmutativa:
Introducción a la propiedad conmutativa del producto de números naturales.
Resumen de la propiedad conmutativa del producto de números naturales.
Propiedad conmutativa del producto de números naturales.
Propiedad asociativa:
Introducción a la propiedad asociativa del producto de números naturales.
Resumen de la propiedad asociativa del producto de números naturales.
Propiedad asociativa del producto de números naturales.
Propiedad distributiva:
Introducción a la propiedad distributiva del producto sobre la suma de números naturales.
Resumen de la propiedad distributiva del producto sobre la suma de números naturales.
Propiedad distributiva del producto sobre la suma de números naturales.
Saca factor común usando la propiedad distributiva del producto sobre la suma de números naturales.
Propiedades de la multiplicación:
Propiedades del producto de números naturales.
Propiedades del producto de números naturales.
Propiedades del producto de números naturales.
Propiedades del producto de números naturales.
Ejemplo: Propiedad distributiva del producto
Alfredo va a comprar cuatro entradas para un concierto de rock y Teresa va a comprar dos entradas . ¿ Cuánto pagarán entre los dos si cada entrada cuesta 15 €?
Podemos resolver el problema de dos formas:
- Primera forma:
- Alfredo----->
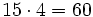
- Teresa------>
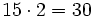
- Total--------->
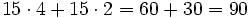 €
€
- Alfredo----->
- Segunda forma:
- Alfredo y Teresa compran 4 + 2 entradas
- Luego en total gastan entre los dos:
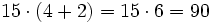 €
€