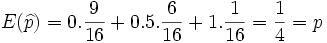Distribuciones muestrales. Teorema central del límite
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:15 6 jul 2007 Juanmf (Discusión | contribuciones) (→Distribución muestral de las proporciones) ← Ir a diferencia anterior |
Revisión de 19:16 6 jul 2007 Juanmf (Discusión | contribuciones) (→Distribución muestral de las proporciones) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| [[imagen:prop3.png|700px]] | [[imagen:prop3.png|700px]] | ||
| </center> | </center> | ||
| - | Calculamos su esperanza matemática y la varianza. | + | |
| - | <math> E( \widehat{p})= 0. \frac{9} {16}+0.5 \frac{6} {16}+1 \frac{1} {16} = \frac{1} {4} | + | Calculamos su esperanza matemática y la varianza: |
| + | |||
| + | <math> E( \widehat{p})= 0. \frac{9} {16} + 0.5. \frac{6} {16} + 1. \frac{1} {16} = \frac{1} {4}= p | ||
| </math> | </math> | ||
Revisión de 19:16 6 jul 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio Indice Estadistica | Inferencia | WIRIS Geogebra Calculadora |
Distribución muestral de las proporciones
Vamos a obtener experimentalmente la distribución de las proporciones muestrales. Para ello consideremos el conjunto de figuras:
Consideremos todas las muestras aleatorias simples (con reemplazamiento) de tamaño 2, y construimos la distribución de probabilidad de la proporción muestral:
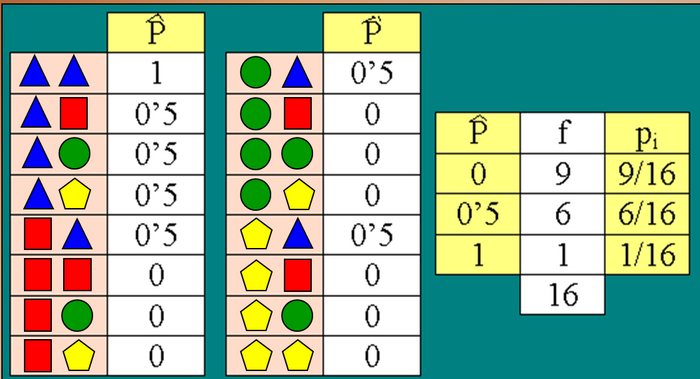
Calculamos su esperanza matemática y la varianza: