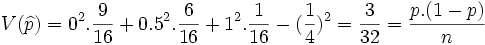Distribuciones muestrales. Teorema central del límite

De Wikipedia

Revisión de 21:46 6 jul 2007 Juanmf (Discusión | contribuciones) (→Distribución muestral de las proporciones) ← Ir a diferencia anterior		Revisión de 21:47 6 jul 2007 Juanmf (Discusión | contribuciones) (→Distribución muestral de las proporciones) Ir a siguiente diferencia →
Línea 42:		Línea 42:
	Si la población es finita y la extracción simultánea o sin reposición, la desviación típica va multiplicada por la siguiente expresión:		Si la población es finita y la extracción simultánea o sin reposición, la desviación típica va multiplicada por la siguiente expresión:
	<center>		<center>
-	<math> \sqrt{ \frac{N - n)} {N - 1}}\right )	+	<math> \sqrt{ \frac{N - n)} {N - 1}}}
	</math></center>		</math></center>
	}}		}}
-
-
	Donde N = tamaño de la población; n = tamaño de la muestra		Donde N = tamaño de la población; n = tamaño de la muestra

---

Revisión de 21:47 6 jul 2007

Distribución muestral de las proporciones

Vamos a obtener experimentalmente la distribución de las proporciones muestrales. Para ello consideremos el conjunto de figuras:

La proporción poblacional de triángulos es 1/4.

Consideremos todas las muestras de tamaño 2 posibles, mediante muestreo aleatorio simple (con reemplazamiento). Hallamos la distribución de probabilidad de la proporción muestral (nombrada por ):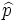

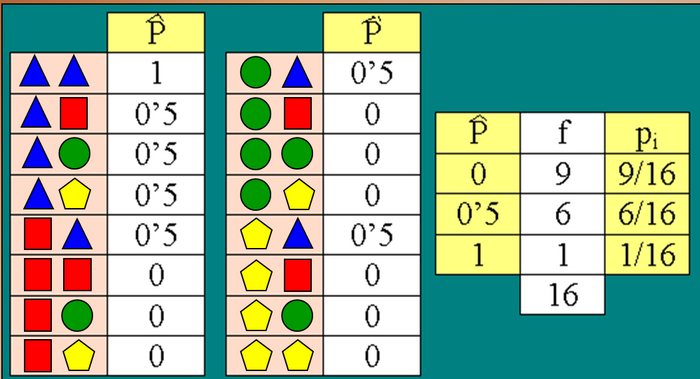
Calculamos su esperanza matemática y la varianza:

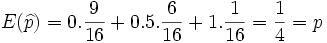
El número de éxitos x de una muestra de tamaño n, se distribuye de forma binomial B(n, p); si la aproximamos a una normal será 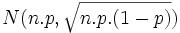. Como 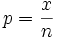, dividiendo x por n se tiene que:

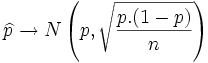Si la población es finita y la extracción simultánea o sin reposición, la desviación típica va multiplicada por la siguiente expresión:

No se pudo entender (error de sintaxis): \sqrt{ \frac{N - n)} {N - 1}}} }}

Donde N = tamaño de la población; n = tamaño de la muestra

Distribución muestral de las medias

Teorema central del límite