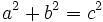Teorema de Pitágoras. Aplicaciones
De Wikipedia
| Revisión de 21:53 14 nov 2007 Juanmf (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 23:05 9 dic 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==Teorema de Pitágoras== | ||
| + | {{Teorema|titulo=Teorema de Pitágoras|enunciado= | ||
| + | En un triángulo rectángulo la hipotenusa al cuadrado es igual al cuadrado de la suma de los catetos | ||
| + | {{Caja|contenido=<math>a^2+b^2=c^2\;\!</math>}} | ||
| + | donde <math>a\;\!</math> y <math>b\;\!</math> son los catetos y <math>c\;\!</math> la hipotenusa. | ||
| + | |demo= | ||
| + | <table align="center"> | ||
| + | <tr> | ||
| + | <td>Fíjate en la figuar de la derecha y observa como el cuadrado grande, de lado <math>a+b</math>, puede descomponerse en un cuadrado de lado <math>c</math> y 4 triángulos rectángulos, como el de partida, de catetos <math>a</math> y <math>b</math> e hipotenusa <math>c</math>. | ||
| + | La superficie del cuadrado grande de lado <math>a+b</math> es: | ||
| + | <center><math>(a+b)^2=a^2+b^2+2ab\;\!</math></center> | ||
| + | La superficie de los cuatro triángulos rectángulos es : | ||
| + | <center><math>4 \cdot \cfrac {b \cdot a}{2}=2ab</math></center> | ||
| + | Restando el área del cuadrado grande de lado <math>a+b</math> menos las areas de los 4 triángulos rectángulos, se obtiene el área del cuadrado de lado <math>c</math>: | ||
| + | <center><math>c^2=(a+b)^2-2ab\;\!</math></center> | ||
| + | Desarrollando el cuadrado del binomio: | ||
| + | <center><math>c^2=(a^2+b^2+2ab)-2ab\;\!</math></center> | ||
| + | De donde obtenemos, simplificando: | ||
| + | <center><math>c^2=a^2+b^2 \;\!</math></center></td> | ||
| + | <td>[[Imagen:pitagoras.png|300px|right]]</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | ----[http://maralboran.ath.cx/web_ma/descartes/3_eso/Demostraciones_graficas_teorema_pitagoras/Demostraciones_1.htm#INTRODUCCIÓN Otras demostraciones gráficas] | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Ternas pitagóricas== | ||
| + | {{Caja_Amarilla|texto=Se llaman '''ternas pitagóricas''' a las ternas de números naturales que verifican el teorema de Pitágoras, por ejemplo 3,4,5. También son ternas pitagóricas sus múltiplos: 6,8,10; 9,12,15 ... | ||
| + | }}{{p}} | ||
| + | {{AI2|titulo=Actividades Interactivas: ''Ternas pitagóricas''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=1. Comprueba las siguientes ternas pitagóricas. | ||
| + | |actividad= | ||
| + | Comprueba que los números 10, 8 y 6 (el doble de 5, 4 y 3) también verifican la relación anterior. Cualquier múltiplo 5*k, 4*k y 3*k de esos tres números (donde k es un número positivo, cualquiera) también la verifican. En el cuadro siguiente varía los valores del parámetro k y comprueba que el triángulo cuyos lados tienen esas medidas siempre es rectángulo y que efectivamente se verifica la relación anterior. Observa que k puede tomar valores decimales. | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/Teorema_de_Pitagoras/pitagoras_3.html | ||
| + | width=500 | ||
| + | height=400 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | ==Aplicaciones del teorema de Pitágoras== | ||
| + | {{AI2|titulo=Actividades Interactivas: ''Aplicaciones del teorema de Pitágoras''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=1. Conocidos los catetos: a=4 cm. y b=5 cm., calcular la hipotenusa, c. | ||
| + | |actividad= | ||
| + | Usaremos el teorema de Pitágoras: | ||
| + | |||
| + | <center><math>c^2=a^2+b^2;\ c^2=4^2+5^2;\ c^2=16+25=13;\ c=\sqrt {41}=6,4</math></center> | ||
| + | |||
| + | Compruébalo en la escena siguiente: | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/Teorema_de_Pitagoras/pitagoras_4.html | ||
| + | width=500 | ||
| + | height=400 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | }} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=2. Conocido un cateto a=5 cm. y la hipotenusa c=8 cm., calcular el otro cateto, b. | ||
| + | |actividad= | ||
| + | Usaremos, de nuevo, el teorema de Pitágoras: | ||
| + | |||
| + | <center><math>c^2=a^2+b^2;\ 8^2=5^2+b^2;\ b^2=64-25=39;\ c=\sqrt {39}=6,25</math></center> | ||
| + | |||
| + | Compruébalo en la escena siguiente: | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/Teorema_de_Pitagoras/pitagoras_4.html | ||
| + | width=500 | ||
| + | height=400 | ||
| + | name=myframe | ||
| + | </iframe></center>}} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=3. Halla la altura de un triángulo equilatero de 4 cm. de lado. | ||
| + | |actividad= | ||
| + | Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Para ello tendrás que mover los vértices del triángulo y usar "la regla" (segmento negro) para medir la altura. | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/geometria/geoweb/trian9_5.html | ||
| + | width=500 | ||
| + | height=370 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| + | }} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=4. Halla la altura de un triángulo isósceles cuyos lados miden c=5 cm. y a=b=4 cm. | ||
| + | |actividad= | ||
| + | Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Para ello tendrás que mover los vértices del triángulo y usar "la regla" (segmento negro) para medir la altura. | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/geometria/geoweb/trian9_5.html | ||
| + | width=500 | ||
| + | height=370 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | ==Clasificar un triángulo atendiendo a sus ángulos, conocidos sus lados== | ||
| + | {{Caja_Amarilla|texto= | ||
| + | En un triángulo cualquiera, si llamamos <math>a</math> al lado mayor, y a los otros dos <math>b</math> y <math>c</math>, se cumple que: | ||
| + | |||
| + | * Si <math>a^2 > b^2 + c^2</math>, el triángulo es obtusángulo | ||
| + | * Si <math>a^2 = b^2 + c^2</math>, el triángulo es rectángulo | ||
| + | * Si <math>a^2 < b^2 + c^2</math>, el triángulo es acutángulo | ||
| + | }}{{p}} | ||
| + | {{AI2|titulo=Actividad Interactiva: ''Clasificar un triángulo conocidos sus lados''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=1. Clasifica los siguientes triángulos: | ||
| + | |actividad='''Clasifica los siguientes triángulos, atendiendo a sus ángulos:''' | ||
| + | |||
| + | '''a) Triángulo de lados 4, 5 y 2.<br>b) Triángulo de lados 5, 3 y 4.<br>c) Triángulo de lados 5, 3 y 3.''' | ||
| + | |||
| + | Primero, en tu cuaderno, haz los cálculos necesarios para contestar a las preguntas. A continuación, en la siguiente escena, mueve los puntos para cambiar el valor de los lados y comprueba los resultados que has obtenido. | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/geometria/geoweb/trian9_3.html | ||
| + | width=500 | ||
| + | height=400 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| <center><iframe> | <center><iframe> | ||
| url=http://http://maralboran.org/web_ma/descartes/Geometria/pitagoras_pgs/Index_Pitagoras.htm | url=http://http://maralboran.org/web_ma/descartes/Geometria/pitagoras_pgs/Index_Pitagoras.htm | ||
Revisión de 23:05 9 dic 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Teorema de Pitágoras
Teorema de Pitágoras
En un triángulo rectángulo la hipotenusa al cuadrado es igual al cuadrado de la suma de los catetos
|
|
donde 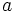 y
y 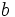 son los catetos y
son los catetos y 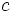 la hipotenusa.
la hipotenusa.
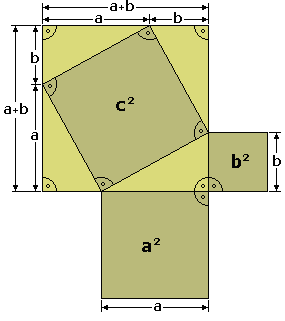
| Fíjate en la figuar de la derecha y observa como el cuadrado grande, de lado a + b, puede descomponerse en un cuadrado de lado c y 4 triángulos rectángulos, como el de partida, de catetos a y b e hipotenusa c.
La superficie del cuadrado grande de lado a + b es: 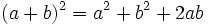 La superficie de los cuatro triángulos rectángulos es : 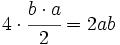 Restando el área del cuadrado grande de lado a + b menos las areas de los 4 triángulos rectángulos, se obtiene el área del cuadrado de lado c: 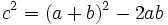 Desarrollando el cuadrado del binomio: 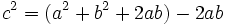 De donde obtenemos, simplificando: 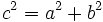 |
Otras demostraciones gráficas
Ternas pitagóricas
Se llaman ternas pitagóricas a las ternas de números naturales que verifican el teorema de Pitágoras, por ejemplo 3,4,5. También son ternas pitagóricas sus múltiplos: 6,8,10; 9,12,15 ...
|
Actividades Interactivas: Ternas pitagóricas
1. Comprueba las siguientes ternas pitagóricas.
Actividad: Comprueba que los números 10, 8 y 6 (el doble de 5, 4 y 3) también verifican la relación anterior. Cualquier múltiplo 5*k, 4*k y 3*k de esos tres números (donde k es un número positivo, cualquiera) también la verifican. En el cuadro siguiente varía los valores del parámetro k y comprueba que el triángulo cuyos lados tienen esas medidas siempre es rectángulo y que efectivamente se verifica la relación anterior. Observa que k puede tomar valores decimales. |
Aplicaciones del teorema de Pitágoras
|
Actividades Interactivas: Aplicaciones del teorema de Pitágoras
1. Conocidos los catetos: a=4 cm. y b=5 cm., calcular la hipotenusa, c.
Actividad: Usaremos el teorema de Pitágoras: 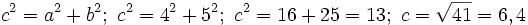 Compruébalo en la escena siguiente:
2. Conocido un cateto a=5 cm. y la hipotenusa c=8 cm., calcular el otro cateto, b.
Actividad: Usaremos, de nuevo, el teorema de Pitágoras: 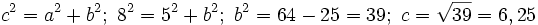 Compruébalo en la escena siguiente:
3. Halla la altura de un triángulo equilatero de 4 cm. de lado.
Actividad: Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Para ello tendrás que mover los vértices del triángulo y usar "la regla" (segmento negro) para medir la altura.
4. Halla la altura de un triángulo isósceles cuyos lados miden c=5 cm. y a=b=4 cm.
Actividad: Resuélvelo en tu cuaderno y compruébalo en la siguiente escena. Para ello tendrás que mover los vértices del triángulo y usar "la regla" (segmento negro) para medir la altura. |
Clasificar un triángulo atendiendo a sus ángulos, conocidos sus lados
En un triángulo cualquiera, si llamamos a al lado mayor, y a los otros dos b y c, se cumple que:
- Si a2 > b2 + c2, el triángulo es obtusángulo
- Si a2 = b2 + c2, el triángulo es rectángulo
- Si a2 < b2 + c2, el triángulo es acutángulo
|
Actividad Interactiva: Clasificar un triángulo conocidos sus lados
1. Clasifica los siguientes triángulos:
Actividad: Clasifica los siguientes triángulos, atendiendo a sus ángulos: a) Triángulo de lados 4, 5 y 2. Primero, en tu cuaderno, haz los cálculos necesarios para contestar a las preguntas. A continuación, en la siguiente escena, mueve los puntos para cambiar el valor de los lados y comprueba los resultados que has obtenido. |