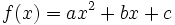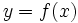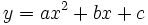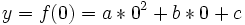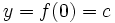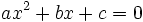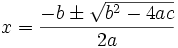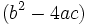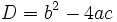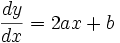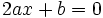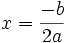Funciones Cuadráticas (PACS)
De Wikipedia
| Revisión de 10:28 27 sep 2008 Juanmf (Discusión | contribuciones) (→Corte con el eje y) ← Ir a diferencia anterior |
Revisión de 10:32 27 sep 2008 Juanmf (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| ==Definición== | ==Definición== | ||
| - | [[Image:Función cuadrática 03.png |right|300px]] | ||
| Una '''función cuadrática''' es la que corresponde a un polinomio en '''x''' de segundo grado, según la forma: | Una '''función cuadrática''' es la que corresponde a un polinomio en '''x''' de segundo grado, según la forma: | ||
| Línea 14: | Línea 13: | ||
| es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de '''a'''. | es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de '''a'''. | ||
| - | + | [[Image:Función cuadrática 03.png |300px]][[Image:Función cuadrática 11.png |300px]] | |
| == Estudio de la función == | == Estudio de la función == | ||
| ==== Corte con el eje y ==== | ==== Corte con el eje y ==== | ||
| - | [[Image:Función cuadrática 11.png |right|300px]] | ||
| - | |||
| La función corta el '''eje y''' en el punto y = f(0), es decir, la parábola corta el eje '''y''' cuando '''x''' vale cero (0): | La función corta el '''eje y''' en el punto y = f(0), es decir, la parábola corta el eje '''y''' cuando '''x''' vale cero (0): | ||
| : <math> y = f(0) = a * 0^2 + b * 0 + c \, </math> | : <math> y = f(0) = a * 0^2 + b * 0 + c \, </math> | ||
| Línea 33: | Línea 30: | ||
| : <math> ax^2 + bx + c = 0 \, </math> | : <math> ax^2 + bx + c = 0 \, </math> | ||
| - | las distintas soluciones de esta [[ecuación de segundo grado]], son los casos de corte con el '''eje x''', que se obtienen como es sabido por la expresión: | + | las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el '''eje x''', que se obtienen como es sabido por la expresión: |
| : <math> x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a} </math> | : <math> x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a} </math> | ||
Revisión de 10:32 27 sep 2008
Tabla de contenidos |
Definición
Una función cuadrática es la que corresponde a un polinomio en x de segundo grado, según la forma:
donde a, b y c son constantes y a distinto de 0.
la representación gráfica en el plano xy haciendo:
esto es:
es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de a.
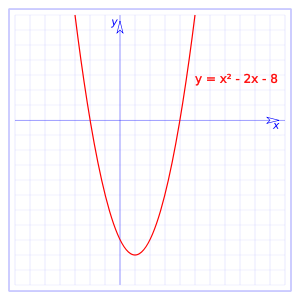
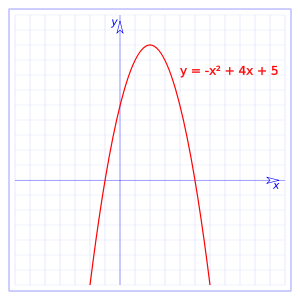
Estudio de la función
Corte con el eje y
La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):
lo que resulta:
la función corta el eje y en el punto (0, c), siendo c el termino independiente de la función.
Corte con el eje x
La función corta al eje x cuando y vale 0:
las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen como es sabido por la expresión:
donde:
se le llama discriminante, D:
según el signo del discriminante podemos distinguir:
- D > 0
La ecuación tiene dos soluciones, por tanto la parábola cortara al eje x en dos puntos: x1, x2
- D = 0
La ecuación tiene una solución, la parábola solo tiene un punto en común con el eje x, en la cual es tangente a este eje donde las dos ramas de la parábola confluyen.
- D < 0
La ecuación no tiene solución real, y la parábola no corta al eje x.
Extremos relativos
Para localizar los extremos relativos, se calcula la derivada de la función, y se iguala a cero, la solución a esta ecuación son los posibles máximos y mínimos de la función, en este caso, partiendo de la función cuadrática:
calculamos su derivada respecto a x:
que si la igualamos a cero, tenemos:
donde x valdrá:
En la vertical que pasa por este valor de x se encontrara el valor máximo o mínimo de la función.