Funciones de Proporcionalidad Inversa (PACS)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 14:20 27 sep 2008 Juanmf (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 14:20 27 sep 2008 Juanmf (Discusión | contribuciones) (→Definición) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| ==Definición== | ==Definición== | ||
| {{Caja Amarilla | {{Caja Amarilla | ||
| - | |texto=La función <math> \ y = \frac{k}{x}</math> , siendo k un número real, es lo que se denomina familia de '''hipérbolas'''. | + | |texto=La función <math> \ y = \frac{k}{x}</math> , siendo <math> \ k </math> un número real, es lo que se denomina familia de '''hipérbolas'''. |
| - | A estas funciones se les llama '''funciones de proporcionalidad inversa''', ya que si <math> \ x </math> e <math> \ y </math> son cantidades correspondientes de dos magnitudes inversamente proporcionales con constante de proporcionalidad k entonces <math> \ x . \ y = \ k </math>. | + | A estas funciones se les llama '''funciones de proporcionalidad inversa''', ya que si <math> \ x </math> e <math> \ y </math> son cantidades correspondientes de dos magnitudes inversamente proporcionales con constante de proporcionalidad <math> \ k </math> entonces <math> \ x . \ y = \ k </math>. |
| Estas hipérbolas en las que las asíntotas son perpendiculares se llaman hipérbolas equiláteras, cuyas ramas son simétricas respecto del origen de coordenadas. | Estas hipérbolas en las que las asíntotas son perpendiculares se llaman hipérbolas equiláteras, cuyas ramas son simétricas respecto del origen de coordenadas. | ||
| }} | }} | ||
Revisión de 14:20 27 sep 2008
Menú:
| Enlaces internos | Para repasar | Enlaces externos |
| Indice CD Alumno 07 Resueltos 07 Descartes Manual Casio | Funciones (ppt) Descartes: Funciones matemáticas | WIRIS Calculadora |
Definición
La función 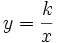 , siendo
, siendo 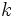 un número real, es lo que se denomina familia de hipérbolas.
un número real, es lo que se denomina familia de hipérbolas.
A estas funciones se les llama funciones de proporcionalidad inversa, ya que si 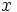 e
e 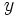 son cantidades correspondientes de dos magnitudes inversamente proporcionales con constante de proporcionalidad
son cantidades correspondientes de dos magnitudes inversamente proporcionales con constante de proporcionalidad 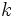 entonces
entonces 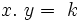 .
.
Estas hipérbolas en las que las asíntotas son perpendiculares se llaman hipérbolas equiláteras, cuyas ramas son simétricas respecto del origen de coordenadas.

