Funciones de Proporcionalidad Inversa (PACS)
De Wikipedia
| Revisión de 14:20 27 sep 2008 Juanmf (Discusión | contribuciones) (→Definición) ← Ir a diferencia anterior |
Revisión de 14:29 27 sep 2008 Juanmf (Discusión | contribuciones) (→Definición) Ir a siguiente diferencia → |
||
| Línea 13: | Línea 13: | ||
| Estas hipérbolas en las que las asíntotas son perpendiculares se llaman hipérbolas equiláteras, cuyas ramas son simétricas respecto del origen de coordenadas. | Estas hipérbolas en las que las asíntotas son perpendiculares se llaman hipérbolas equiláteras, cuyas ramas son simétricas respecto del origen de coordenadas. | ||
| + | }} | ||
| + | {{AI2|titulo=Actividades Interactivas: ''Función proporcionalidad invers'' | ||
| + | |cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=1. Representación gráfica de la función de proporcionalida inversa | ||
| + | |actividad= | ||
| + | Pulsa el botón inicio y escribe a continuación de k los valores: -4, -3, -2, -1, 1, 2, 3, 4. | ||
| + | |||
| + | Anota en tu cuaderno de trabajo las respuesta que obtengas a las siguientes cuestiones: | ||
| + | |||
| + | ¿Cómo cambia la hipérbola al pasar de valores negativos a positivos del parámetro k? | ||
| + | ¿Para qué valores de k las ramas de la hipérbola se separan más del origen de coordenadas?. | ||
| + | ¿Qué sucede cuando k=0?. | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://www.maralboran.org/web_ma/descartes/Analisis/La_hiperbola/La_hiperbola2.htm | ||
| + | width=100% | ||
| + | height=1000 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | }} | ||
| }} | }} | ||
Revisión de 14:29 27 sep 2008
| Enlaces internos | Para repasar | Enlaces externos |
| Indice CD Alumno 07 Resueltos 07 Descartes Manual Casio | Funciones (ppt) Descartes: Funciones matemáticas | WIRIS Calculadora |
Definición
La función 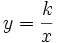 , siendo
, siendo 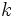 un número real, es lo que se denomina familia de hipérbolas.
un número real, es lo que se denomina familia de hipérbolas.
A estas funciones se les llama funciones de proporcionalidad inversa, ya que si 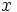 e
e 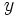 son cantidades correspondientes de dos magnitudes inversamente proporcionales con constante de proporcionalidad
son cantidades correspondientes de dos magnitudes inversamente proporcionales con constante de proporcionalidad 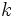 entonces
entonces 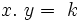 .
.
Estas hipérbolas en las que las asíntotas son perpendiculares se llaman hipérbolas equiláteras, cuyas ramas son simétricas respecto del origen de coordenadas.
|
Actividades Interactivas: Función proporcionalidad invers
1. Representación gráfica de la función de proporcionalida inversa
Actividad: Pulsa el botón inicio y escribe a continuación de k los valores: -4, -3, -2, -1, 1, 2, 3, 4. Anota en tu cuaderno de trabajo las respuesta que obtengas a las siguientes cuestiones: ¿Cómo cambia la hipérbola al pasar de valores negativos a positivos del parámetro k? ¿Para qué valores de k las ramas de la hipérbola se separan más del origen de coordenadas?. ¿Qué sucede cuando k=0?. |

