Función biyectiva
De Wikipedia
Revisión de fecha 10:13 13 dic 2016; Ver revisión actual
← Revisión anterior | Revisión siguiente →
← Revisión anterior | Revisión siguiente →
Una función 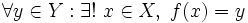 Equivalentemente, una función es biyectiva si es al mismo tiempo inyectiva y sobreyectiva. |
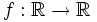 , dada por
, dada por 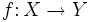 es biyectiva si cada valor de
es biyectiva si cada valor de 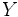 se corresponde con un único valor de
se corresponde con un único valor de 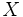 . Simbólicamente:
. Simbólicamente:
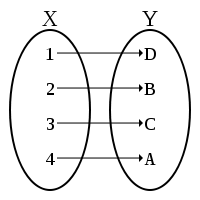
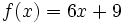 es biyectiva.
es biyectiva.
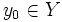 , podemos despejar
, podemos despejar  de la expresión
de la expresión 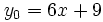 , para obtener el valor
, para obtener el valor 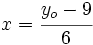 , que es el único que se corresponde con
, que es el único que se corresponde con 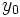 .
.
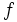 es una función biyectiva, entonces su
es una función biyectiva, entonces su 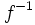 existe y también es biyectiva.
existe y también es biyectiva.

