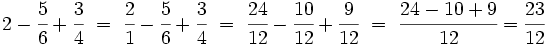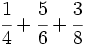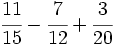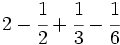Fracciones: Suma y resta (1º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 138)
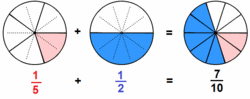
Suma y resta de fracciones con el mismo denominador
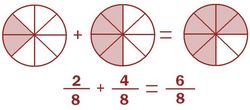
Procedimiento Para sumar o restar fracciones con el mismo denominador, sumamos o restamos los numeradores y dejamos el mismo denominador Suma o resta de fracciones con el mismo denominador. Suma de fracciones con el mismo denominador. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta. Suma y resta de fracciones con el mismo denominador. Suma y resta de fracciones con el mismo denominador. |
Suma y resta de fracciones con distinto denominador
Procedimiento Para sumar o restar fracciones con distinto denominador, primero se reducen las fracciones a común denominador y luego se procede como en el caso en el que las fracciones tienen el mismo denominador. |
Otro método para sumar o restar fracciones fácil de recordar pero que requiere simplificar más.
Suma y resta de fracciones con distinto denominador.
Suma y resta de fracciones con distinto denominador.
Suma y resta de fracciones con distinto denominador.
Suma de fracciones por el método del m.c.m.
Suma y resta de fracciones por el método del m.c.m.
Suma y resta de fracciones. Propiedades.
Suma y resta de fracciones con o sin paréntesis.
Ejercicios propuestos
|
Ejercicios propuestos: Suma y resta de fracciones |
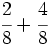 b)
b) 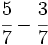
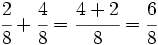
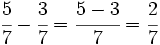
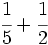 b)
b) 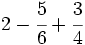
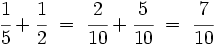 (Ver Fig. 2)
(Ver Fig. 2)