Radicales (1ºBach)
De Wikipedia
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Raíces
Sdefine raíz n-sima de un número real 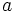 (y se representa por
(y se representa por ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) ) como otro número real
) como otro número real 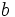 tal que
tal que 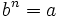 .
. 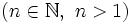
Es decir:
![b=\sqrt[n]{a} \iff b^n =a](/wikipedia/images/math/a/8/5/a854f42279a8ade5b0082bc477d30b79.png)
El número 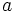 se llama radicando, el número
se llama radicando, el número 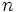 , índice y
, índice y 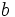 es la raíz.
es la raíz.
La raíz como potencia de exponente fraccionario
Proposición
- Toda raíz se puede expresar como una potencia cuya base es el radicando,
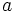 , y el exponente es
, y el exponente es 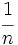 , siendo
, siendo 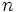 el índice de la raíz. Ésto es:
el índice de la raíz. Ésto es:
|
|
- De forma similar, también se cumple:
|
|
Demostración:
Para la primera parte, basta con ver que se cumple la condición de la definición de raíz.
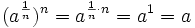
Para la segunda parte, haremos una comprobación análoga:
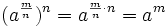
Ejemplos:
Pulsa el botón "Ejemplo" para ver distintos ejemplos y anótalos en tu cuaderno:
Ejemplo: La raíz como potencia de exponente fraccionario
- Escribe las siguientes potencias de exponente fraccionario en forma de raíces y calcula su valor:
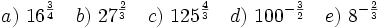
Solución:
Utiliza la siguiente escena para comprobar su resultado. Aumenta el número de decimales cuando sea necesario.
![\sqrt[n]{a}=a^\frac{1}{n}](/wikipedia/images/math/2/0/0/2009af813099ac7b1bef0f0fb92a7999.png)
![\sqrt[n]{a^m}=a^\frac{m}{n}](/wikipedia/images/math/3/b/0/3b0234682d54453ceee722e89c782c2e.png)

