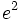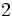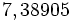Funciones exponenciales (1ºBach)
De Wikipedia
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Función exponencial de base a
Sea 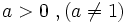 un número real. Se define la función exponencial de base
un número real. Se define la función exponencial de base  como:
como:
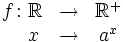
La función exponencial de base e (número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
|
Actividad Interactiva: Función exponencial
Actividad 1. Representación gráfica de distintas funciones exponenciales.
Actividad: En esta escena tienes las gráfica de las funciones: a)
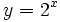 (en verde); b) (en verde); b) 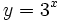 (en amarillo); c) (en amarillo); c) 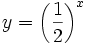 (en rojo); d) (en rojo); d) 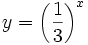 (en turquesa) (en turquesa)Comprueba en la escena anterior las siguientes propiedades:
|
Propiedades
Las funciones exponenciales de base  cumplen las siguientes propiedades:
cumplen las siguientes propiedades:
- Son continuas en
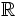 .
.
- Pasan por
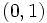 y
y 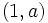 .
.
- Si
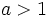 son crecientes y si
son crecientes y si 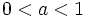 son decrecientes. Su crecicmiento supera al de cualquier función potencia.
son decrecientes. Su crecicmiento supera al de cualquier función potencia.
- Son positivas y nunca se anulan (su gráfica está por encima del eje X).
Calculadora
Exponencial de base 10
|
Calculadora: Exponencial de base 10 |
Exponencial de base e
|
Calculadora: Exponencial de base e |
Crecimiento exponencial
El término crecimiento exponencial se aplica generalmente a una magnitud 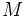 que crece con el tiempo
que crece con el tiempo 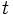 de acuerdo con la ecuación:
de acuerdo con la ecuación:
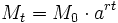
Ejemplos:
Los siguientes fenómenos siguen un crecimiento exponencial:
- El número de células de un feto mientras se desarrolla en el útero materno.
- En una economía sin trastornos, los precios crecen exponencialmente, donde la tasa coincide con el índice de inflación.
- El número de contraseñas posibles con n dígitos crece exponencialmente con n.
- El número de bacterias que se reproducen por mitosis.
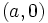 , donde
, donde 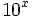 usaremos la tecla
usaremos la tecla 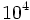
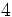
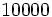
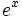 usaremos la tecla
usaremos la tecla