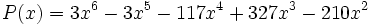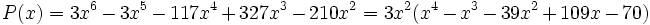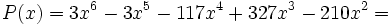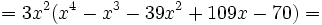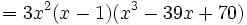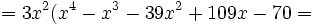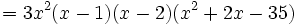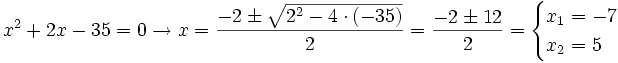Plantilla:Factorización de un polinomio mediante la regla de Ruffini
De Wikipedia
Para factorizar un polinomio mediante la regla de Ruffini, aplicaremos ésta sucesivamente, utilizando como candidatos a raíces los divisores del término independiente, hasta que nos quede un polinomio de segundo grado. Cuando estemos en este punto, aplicaremos la fórmula de la ecuación de segundo grado y obtendremos las dos últimas raíces y por tanto los dos últimos factores. Esto será así, siempre y cuando, el discriminante de la ecuación no sea negativo, ya que de serlo, no habrá más raíces y no podremos descomponerlo más.
Ejemplo: Factorización de polinomios
Factoriza el siguiente polinomio:
Primero sacamos factor común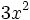 
:
Ahora aplicamos Ruffini. Los divisores de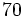 
son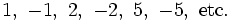 
Empezaremos probando con el 1:
| 1 -1 -39 109 -70
|
1| 1 0 -39 70
--|----------------------
| 1 0 -39 70 |0
|____
Como el resto es cero, hemos encontrado una de las raíces,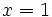 
y uno de los factores 
.
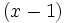Seguimos aplicando Ruffini. Probamos con 1, de nuevo ya que podría repetirse dicha raíz:
| 1 0 -39 70
|
1| 1 1 38
--|-----------------
| 1 1 38 |108
|____
El resto es diferente de cero con lo que tenemos que seguir probando, con el -1:
| 1 0 -39 70
|
-1| -1 1 38
--|-----------------
| 1 -1 -38 |108
|____
El resto vuelve a ser diferente de cero, probamos con 2:
| 1 0 -39 70
|
2| 2 4 -70
--|----------------
| 1 2 -35 |0
|____
Ya hemos encontrado otra raíz,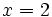 
, y el factor correspondiente, 
.
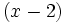El polinomio quedará de la siguiente forma:
Finalmente para encontrar las dos últimas raíces utilizamos la fórmula de la ecuación de 2º grado:
Así, sus raíces son 5 y -7 y sus factores (x-5) y (x+7).
De esta manera:
