Plantilla:La sucesión de Fibonacci y el número áureo
De Wikipedia
La sucesión de Fibonacci y el número áureo Si a partir de la sucesión de Fibonacci 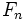 = 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,..., = 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...,construimos, por recurrencia, la sucesión 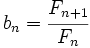 Entonces, esta sucesión tiende al número áureo: 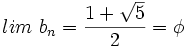 Demostración: Comprobación: Si en la sucesión de Fibonacci 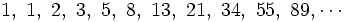 dividimos cada término entre el anterior, tenemos: 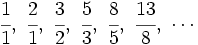 que expresada con decimales nos da: 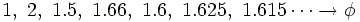 Demostración: Por construcción de la sucesión de Fibonacci: 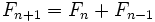 Dividiendo ambos miembros por 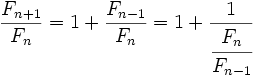 Tomando límites en ambos miembros: 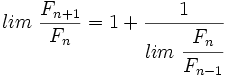 Llamando 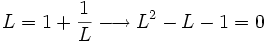 ecuación de segundo grado cuya única raíz válida es: 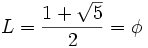 |
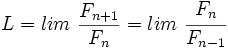 , tenemos:
, tenemos:


