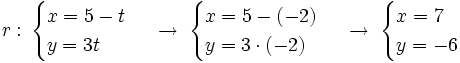Posiciones relativas de dos rectas del plano (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 200)
Posición relativa de dos rectas en el plano
Dadas las ecuaciones de dos rectas del plano, éstas pueden ser secantes, paralelas o coincidentes.
Veamos como se averigua dependiendo del tipo de ecuaciones que nos den.
Posición relativa de dos rectas dadas en ecuaciones paramétricas
Procedimiento
Dadas las rectas: 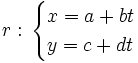 y
y 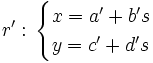
para hallar su posición relativa igualaremos las incógnitas y resolveremos el siguiente sistema de dos ecuaciones con dos incógnitas, 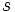 y
y 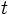 :
:
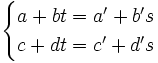
- Si el sistema es compatible determinado (una solución:
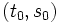 ), las dos rectas se cortan en un punto, que se obtiene sustituyendo los parámetros
), las dos rectas se cortan en un punto, que se obtiene sustituyendo los parámetros 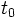 y
y 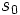 , en las ecuaciones paramétricas.
, en las ecuaciones paramétricas.
- Si el sistema es incompatible (no tiene solución), las dos rectas son paralelas.
- Si el sistema es compatible indeterminado (infinitas soluciones) las rectas son coincidentes.
Ejemplo: Posición relativa de dos rectas
Determina la posición relativa de las rectas: 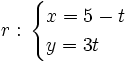 y
y 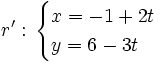
Hay que cambiar el parámetro "t" en una de las dos ecuaciones (por ejemplo la segunda) por otro distinto "s".
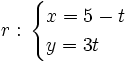 ;
; 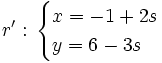
A continuación se resuelve el siguiente sistema:
Luego las rectas son secantes, y su punto de corte lo obtenemos sustituyendo estas soluciones en cualquiera de las dos ecuaciones paramétricas, por ejemplo, en la primera:
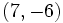 .
.Posición relativa de dos rectas dadas en ecuaciones implícitas
Procedimiento
Dadas las rectas: 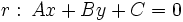 y
y 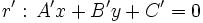
para hallar su posición relativa resolveremos el siguiente sistema de dos ecuaciones con dos incógnitas:, 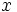 e
e 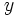 :
:
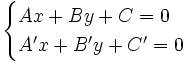
- Si el sistema es compatible determinado (una solución:
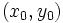 ), las dos rectas se cortan en ese punto. (Esto ocurre cuando
), las dos rectas se cortan en ese punto. (Esto ocurre cuando 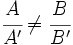 ).
).
- Si el sistema es incompatible (no tiene solución), las dos rectas son paralelas. (Esto ocurre cuando
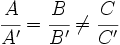 ).
).
- Si el sistema es compatible indeterminado (infinitas soluciones) las rectas son coincidentes. (Esto ocurre cuando
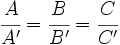 ).
).
Ejemplo: Posición relativa de dos rectas
Determina la posición relativa de las rectas: 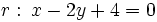 y
y 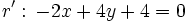
Hay que resolver el siguiente sistema.
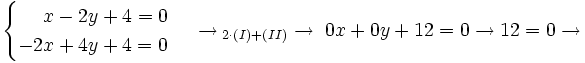 No tiene solución.
No tiene solución.
Posición relativa de dos rectas dadas en ecuaciones explícitas
Procedimiento
Dadas las rectas: 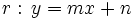 y
y 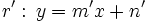
para hallar su posición relativa resolveremos el siguiente sistema de dos ecuaciones con dos incógnitas:, 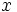 e
e 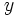 :
:
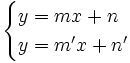
- Si el sistema es compatible determinado (una solución:
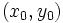 ), las dos rectas se cortan en ese punto. (Esto ocurre cuando las pendientes son distintas:
), las dos rectas se cortan en ese punto. (Esto ocurre cuando las pendientes son distintas: 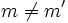 ).
).
- Si el sistema es incompatible (no tiene solución), las dos rectas son paralelas. (Esto ocurre cuando
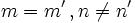 ).
).
- Si el sistema es compatible indeterminado (infinitas soluciones) las rectas son coincidentes. (Esto ocurre cuando
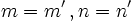 ).
).
Videotutoriales
Videotutorial
Videotutorial
Videotutorial