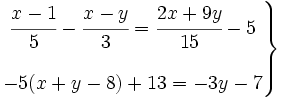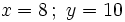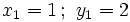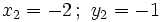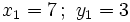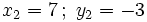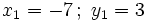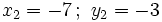Resolución de sistemas lineales y no lineales (3ºESO Académicas)
De Wikipedia
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 131)
Reglas para resolver sistemas lineales
Procedimiento
Para resolver un sistema de ecuaciones lineales podemos proceder de la siguiente forma:
- Transformar las ecuaciones del sistema hasta que tengan la forma
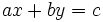 . Para ello deberás quitar denominadores y paréntesis (si los hay), transponer términos y simplificar.
. Para ello deberás quitar denominadores y paréntesis (si los hay), transponer términos y simplificar.
- Elegir un método de resolución adecuado: el método de sustitución es cómodo si alguna incógnita tiene coeficiente 1 o -1; el de reducción es cómodo si alguna incógnita tiene el mismo coeficiente en las dos ecuaciones o sus coeficientes son uno múltiplo del otro; el de igualación es cómodo por su mecánica de despejar, igualar y multiplicar en cruz.
- Podemos, opcionalmente, comprobar las soluciones. Para ello sustituiremos las incógnitas por los valores obtenidos en las dos ecuaciones del sistema de partida y los resultados deben coincidir.
Resolución de sistemas no lineales
Para resolver sistemas no lineales también podemos usar los métodos algebraicos de sustitución, igualación y reducción.
Ejercicios resueltos:
Resuelve los siguientes sistemas:
- 1.
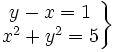
- 2.
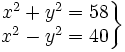
Solución:
Soluciones:
1. Tiene dos soluciones:
2. Tiene cuatro soluciones:
Ejercicios propuestos
|
Ejercicios y problemas propuestos: Resolución de sistemas no lineales |
Resolución de problemas mediante sistemas
Procedimiento
Para resolver un problema mediante sistemas de ecuaciones hay que seguir los siguientes pasos:
- Determinar las incógnitas.
- Traducir el enunciado del problema al lenguaje algebraico mediante ecuaciones en las que intervengan las incógnitas.
- Resolver el sistema, es decir, hallar el valor de las incógnitas.
- Dar la solución del problema a partir de los valores obtenidos de las incógnitas.
Ejercicios propuestos
|
Ejercicios y problemas propuestos: Resolución de problemas mediante sistemas |