Áreas y perímetros de figuras curvas (3ºESO Académicas)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 195)
Círculo
- Área de un circulo y longitud de una circunferencia.
- Longitud de un arco de circunferencia y área del sector circular.
- Ejemplos.
Área de un circulo y longitud de una circunferencia. Ejemplos.
El círculo, su área y su perímetro. Ejemplos
Cálculo del perímetro del círculo o longitud de la circunferencia.
Cálculo del área del círculo.
La longitud de la circunferencia y el número Pi. ¿Cómo calcular el número Pi de forma aproximada?
La circunferencia y el círculo. Elementos de la circunferencia. El número pi y el perímetro del círculo. Ejemplos.
Obtención del área del círculo como aproximación del área de un polígono.
Área del círculo y perímetro de la circunferencia.
Obtener el área de un círculo que posee un diámetro de 30 cm.
Obtener el perímetro de un círculo que posee un radio de 3 m.
Obtener el radio de un círculo que posee una circunferencia de 17.2788 pies.
Una máquina de dulces hace monedas de chocolate circulares. El diámetro de cada monedas es de 16 milímetros. ¿Cuál es el área de cada moneda?
Determinar el diámetro y el área de un círculo cuya circunferencia mide 188.4 cm
Si tienes un cuadrado de 15 cm de lado, calcula las longitudes de las circunferencias inscrita y circunscrita.
Si un arco de 180º tiene por longitud 120 cm, calcula la longitud de la circunferencia.
Si tienes una circunferencia circunscrita en un cuadrado de lado 8 cm, calcula su longitud y el perímetro del cuadrado.
Una rueda de bicicleta tiene 45 cm de radio. Calcula la longitud que recorrerá la rueda después de 200 vueltas.
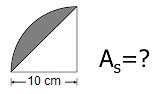
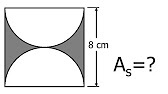
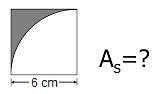
Halla el área coloreada de la figura.
Acertijo que plantea un problema similar al siguiente: Supongamos que la Tierra es esférica y que la rodeamos con una cuerda por el ecuador. Si alargamos esa cuerda un metro poniéndola como un círculo en torno a la Tierra. ¿Crees que habrá espacio suficiente para que pase un conejo por el hueco?
En el acertijo planteado en el video, la cuerda se alarga 20 m y nos pregunta si podríamos pasar por debajo de ella sin agacharnos.
En esta escena podrás deducir la fórmula de la longitud de la circunferencia de forma aproximada.
En esta escena podrás deducir la fórmula del área del círculo "pelándolo".
Actividad en la que podrás ver como se obtiene la longitud de la circunferencia. También podrás hacer unos tests.
Actividades en las que podrás ver como se puede aproximar el área del círculo y la longitud de la circunferencia a partir del área y perímetro de polígonos regulares de muchos lados.
Halla la longitud de un arco de circunferencia.
¿Cuántos metros avanza una rueda de 30 cm de radio al dar una vuelta?
El diámetro de un círculo mide 20 dm. ¿Cuántos decímetros cuadrados mide su área?
Ejercicios de autoevaluación sobre el área del círculo.
Ejercicios de autoevaluación sobre el área del círculo.
Ejercicios de autoevaluación sobre el área del círculo y la longitud de la circunferencia.
|
Actividad: El círculo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
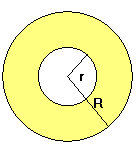
Corona circular
Fórmula del área de la corona circular. Ejemplo.
Deducción de la fórmula del área de la corona circular. Ejemplo.
Halla el área de una corona circular de radio mayor, 50 m, y radio menor, 15 m.
Halla el área de una corona circular de radio mayor, 9 cm, y radio menor, 6 cm.
Halla el perímetro de una corona circular de radio mayor, 5 cm, y radio menor, 2 cm.
En esta escena podrás hallar el área de la corona circular.
Sector circular
La fórmula del área del sector circular se obtiene a partir de la del área del círculo, aplicando una regla de tres.
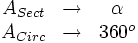
Despejando el área del sector:
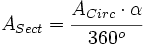
de donde, sustituyendo el área del círculo por su valor, 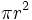 , se obtiene la fórmula.
, se obtiene la fórmula.
Lo mismo ocurre con la de la longitud del arco, que se obtiene a partir de la de la longitud de la circunferencia, también mediante una regla de tres.
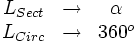
Despejando la longitud del sector:
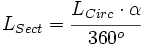
de donde, sustituyendo la longitud de la circunferencia por su valor, 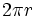 , se obtiene la fórmula.
, se obtiene la fórmula.
Obtención del área de un sector circular. Ejemplo
Fórmula que permite calcular el área de un sector circular a partir del valor del ángulo central. Ejercicios. (Nivel 1)
Fórmula que permite calcular el área de un sector circular a partir del valor del ángulo central. Ejercicios. (Nivel 2)
Fórmula que permite calcular la longitud de un arco de circunferencia a partir del valor del ángulo central. Ejercicios. (Nivel 3)
Fórmula que permite calcular la longitud de un arco de circunferencia a partir del valor del ángulo central. Ejercicios. (Nivel 1)
2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 2)
2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 3)
Deducción de la fórmula del área del trapecio circular. Ejemplo.
En esta escena podrás hallar el área del sector circular y la longitud del arco de circunferencia correspondiente.
|
Actividad: El sector circular
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
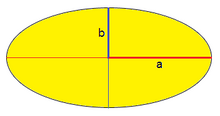
Elipse
|
|
En esta escena podrás hallar el área y el perímetro aproximado de la elipse.
Ejercicios propuestos
|
Ejercicios propuestos: Áreas de figuras curvas |
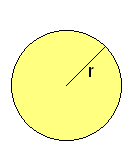
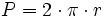
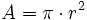
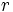 : radio.
: radio.
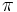 : número Pi = 3,14159...
: número Pi = 3,14159...
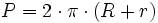
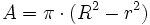
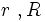 : radios respectivos.
: radios respectivos.
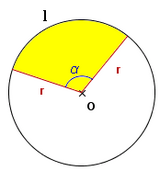
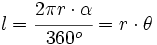
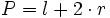
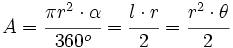
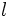 : arco.
: arco.
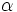 : ángulo (en grados sexagesimales).
: ángulo (en grados sexagesimales).
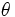 : ángulo
: ángulo 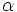 (en radianes).
(en radianes).
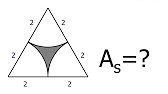
![P \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,](/wikipedia/images/math/4/5/3/4531867e543bc27be7c45f80a7599da1.png)
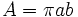
 : semieje mayor.
: semieje mayor.
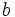 : semieje menor.
: semieje menor.

