Familias de funciones elementales (1ºBach)
De Wikipedia
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Funciones algebraicas y trascendentes
- Las funciones algebraicas son aquellas en las que las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
- Las funciones trascendentes son aquellas que no son algebraicas.
La función "f" se dice "algebraica" si las operaciones que deben realizarse para determinar el número real "f(x)" son las llamadas algebraicas: suma, resta, multiplicación, división, potenciación de exponente constante y radicación de ínidice constante. Si "f" no es algebraica, se dice "trascendente".
Funciones lineales
Representación de la familia de funciones lineales.
Funciones cuadráticas
Representación de la familia de funciones cuadráticas.
Funciones raíz
Funciones de proporcionalidad inversa
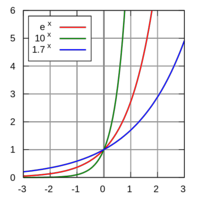
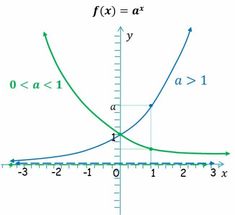
Funciones exponenciales
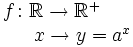
|
Propiedades
Propiedades de la función exponencial Las funciones exponenciales de base
|
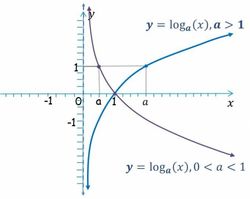
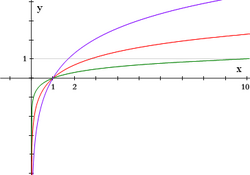
Funciones logarítmicas
Sea 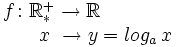
|
Propiedades
Propiedades de la función logarítmica Las funciones exponenciales de base
|
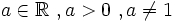 . Se define la función exponencial de base
. Se define la función exponencial de base  como:
como:
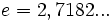 (número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
(número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
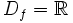 .
.
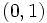 y
y 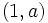 .
.
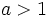 son crecientes
son crecientes
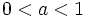 son decrecientes.
son decrecientes.
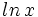 .
.
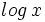 (sin especificar la base).
(sin especificar la base).
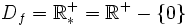 .
.
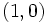 y
y 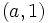 .
.
![\sqrt[n]{x}](/wikipedia/images/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) .
.
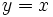 .
.