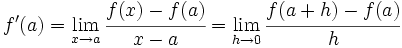Crecimiento de una función en un punto. Derivada (2ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Tasa de variación media
Para medir el crecimiento medio de una función en un intervalo [a,b], se utiliza la tasa de variación media (T.V.M.) o tasa de cambio, que se define como el cociente de la variación de y entre la variación de x:
Si hacemos
Proposición La T.V.M. de una función en un intervalo |
- Definición de tasa de variación media de una función.
- Ejemplo a partir de la gráfica de la función.
- Ejemplo a partir de la expresión analítica de la función.
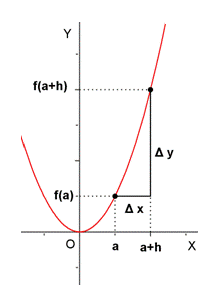
- Definición de tasa de variación media o tasa de cambio de una función f en el intervalo [a,a+h].
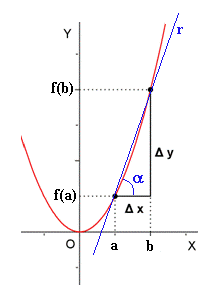
- Interpretación geométrica.
- Ejemplos
Algunos ejemplos que relacionan el concepto de tasa de variación media con el de velocidad media.
Tasa de variación media de una recta
Tasa de variación media de una parábola. Interpretación con un ejemplo de la vida cotidiana.
Calcula la T.V.M. de f(x) = x2 + 2; en [1,4].
Calcula la T.V.M. de:
- a) d(t) = 3t + 1; en [0,1] y [1,2].
- b) d(t) = t2 + 1; en [0,3] y [2,3].
A partir de la gráfica, determina el intervalo en el cual la T.V.M. de la función es -4.
A partir de la tabla, determina la T.V.M. de la función en el intervalo [-5, -2].
Dada la función 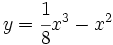 , ¿sobre cuál de los siguientes intervalos tiene T.V.M. igual a 1/2: [-2, 2], [0, 4], [-3, 2], [-4, 1] ?
, ¿sobre cuál de los siguientes intervalos tiene T.V.M. igual a 1/2: [-2, 2], [0, 4], [-3, 2], [-4, 1] ?
Cálcula la T.V.M. de 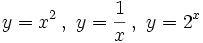 en el intervalo [x, x+h].
en el intervalo [x, x+h].
Problema sobre el cálculo de la tasa de variación media a partir de una tabla.
Problema sobre el cálculo de la tasa de variación media a partir de una gráfica.
Problema sobre el cálculo de la tasa de variación media.
Tasa de variación media.
En esta escena podrás calcular la T.V.M. de la función que tú quieras.
Tasa de variación media.
Problemas verbales sobre la tasa de variación media.
Crecimiento de una función en un punto. Derivada
- El crecimiento de una función
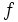 en un intervalo
en un intervalo ![[a,b]\;](/wikipedia/images/math/9/a/e/9ae0a6959368a1b0c6be4a9feb1e9b5c.png) se mide mediante la pendiente de la recta que pasa por los puntos
se mide mediante la pendiente de la recta que pasa por los puntos 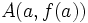 y
y 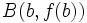 , es decir, mediante
, es decir, mediante ![T.V.M._f[a,b]\;](/wikipedia/images/math/1/b/0/1b099a5cc384e6e5cd2dce91dc815fa8.png) .
.
- El crecimiento de una función
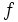 en un punto de abscisa
en un punto de abscisa  se mide mediante la pendiente de la recta tangente a la curva en dicho punto. A dicho valor se le llama derivada de
se mide mediante la pendiente de la recta tangente a la curva en dicho punto. A dicho valor se le llama derivada de 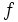 en el punto
en el punto  y se expresa
y se expresa 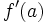 .
.
Ejercicios propuestos
|
Ejercicios propuestos: Crecimiento en un punto. Derivada |
Obtención de la derivada de una función en un punto
Hemos dicho que la derivada de una función 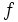 en un punto
en un punto  es la pendiente de la recta tangente a la curva en dicho punto, y se representa
es la pendiente de la recta tangente a la curva en dicho punto, y se representa 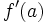 . Podemos obtener dicho valor mediante el concepto de límite:
. Podemos obtener dicho valor mediante el concepto de límite:
En esta escena podrás ver cómo se interpreta geométricamente el concepto de derivada de una función en un punto.
Ejemplos: Derivada de una función en un punto
Calcula la derivada de la función 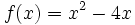 en el punto de abscisa
en el punto de abscisa 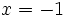
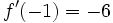
La derivada. Un poco de historia y explicación gráfica.
Un ejemplo de móviles para explicar qué es la derivada.
La derivada en términos geométricos.
Aproximación intuitiva al concepto de función derivable.
Apróximación al concepto de derivada apoyándonos en la existencia o no de la recta tangente en un punto.
Definición rigurosa de derivada de una función en un punto.
Halla la derivada de la función 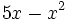 en los puntos x=4 y x=5.
en los puntos x=4 y x=5.
Halla la derivada de 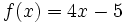 en el punto x=2.
en el punto x=2.
Halla la derivada de 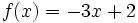 en el punto x=-1.
en el punto x=-1.
Halla la derivada de 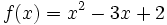 en el punto x=4.
en el punto x=4.
Halla la derivada de 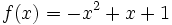 en el punto x=-2.
en el punto x=-2.
Halla la derivada de 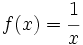 en el punto x=2.
en el punto x=2.
Halla la derivada de 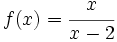 en el punto x=1.
en el punto x=1.
Halla la derivada de 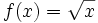 en el punto x=9.
en el punto x=9.
Ejercicios propuestos
|
Ejercicios propuestos: Derivada de una función en un punto |
![T.V.M._f \,[a,b]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(b)-f(a)}{b-a}](/wikipedia/images/math/8/9/c/89c85ce438b13f83f07e3480026d5be8.png)
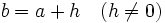 , la expresión anterior queda como sigue:
, la expresión anterior queda como sigue:
![T.V.M._f \,[a,a+h]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(a+h)-f(a)}{h}](/wikipedia/images/math/c/8/1/c81e647a1a3e3e683857d6714eed390f.png)
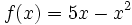 , su T.V.M. en el intervalo [1,2] es:
, su T.V.M. en el intervalo [1,2] es:
![T.V.M._f \,[1,2]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(2)-f(1)}{2-1}=\cfrac{6-4}{1}=2](/wikipedia/images/math/1/4/1/141dc581dee9a22c26e10a24407de907.png)
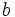 .
.
![T.V.M._f \,[a,b]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=tg\, \alpha=m](/wikipedia/images/math/6/b/7/6b761a6a89fc5990f82ffd9ae6ec3b0e.png)
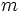 es la pendiente de la recta r.
es la pendiente de la recta r.