Volumen del prisma y del cilindro (2º ESO)
De Wikipedia
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 244)
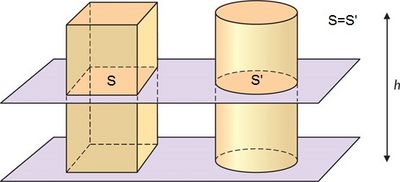
Principio de Cavalieri
Principio de Cavalieri
Si dos cuerpos tienen la misma altura y además tienen igual área en sus secciones planas realizadas a una misma altura, entonces tienen el mismo volumen.
Estas dos figuras tienen el mismo volumen por el principio de Cavalieri
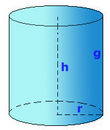
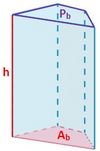
Volumen del prisma y del cilindro
- Una figura prismática es aquella que tiene dos bases iguales paralelas y al cortarla mediante planos paralelos a las bases se obtienen secciones idénticas a ellas.
- Las figuras prismáticas más conocidas son los prismas y el cilindro.
Corolario
El volumen de los prismas y los cilindros, al ser figuras prismáticas, es igual al área de la base por la altura.
|
|
|
|
|
Ejercicios propuestos
|
Ejercicios propuestos: Volumen del prisma y del cilindro |
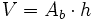
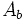 : Área de la base.
: Área de la base.
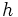 : altura.
: altura.
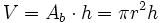
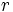 : radio.
: radio.