Volumen del prisma y del cilindro (2º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 244)
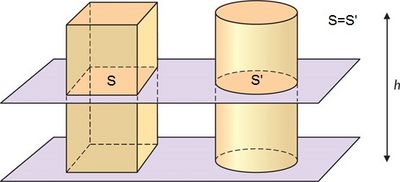
Principio de Cavalieri
Principio de Cavalieri
Si dos cuerpos tienen la misma altura y además tienen igual área en sus secciones planas realizadas a una misma altura, entonces tienen el mismo volumen.
Volumen del prisma y del cilindro
- Una figura prismática es aquella que tiene dos bases iguales paralelas y al cortarla mediante planos paralelos a las bases se obtienen secciones idénticas a ellas.
- Las figuras prismáticas más conocidas son los prismas y los cilindros.
Apoyándonos en el principio de Cavalieri, tenemos los siguientes resultados:
Proposición
- El volumen de una figura prismática es igual al área de la base por la altura.
- El volumen de los prismas y los cilindros, al ser figuras prismáticas, es igual al área de la base por la altura.
Volumen del prisma
|
|
Plantilla:Videos: Volumen del prisma
- 0:00-1:40: Definición de prisma recto.
- 1:30-4:12 :Superficie lateral del prisma recto.
- 4:12-5:12 :Superficie total del prisma recto.
- 5:12-6:09 :Volumen del prisma recto.
- 6:09-12:54: Problema: Halla el área lateral, el área total y el volumen de un prisma triangular regular de 5 cm de arista básica y 7 cm de altura.
Cálculo del área total y el volumen de un prisma. Ejemplos.
Área y volumen del prisma recto.
En este vídeo de MasterD, se pretende dejar claros todos los conceptos relacionados con los prismas. Daremos una definición, explicaremos cuáles son sus partes, veremos cómo se pueden clasificar con algunos ejemplos y finalmente pasaremos a ver el área y el volumen.
Cálculo del volumen y la superficie de un prisma.
Aviso: El vídeo habla de los cilindros como un caso especial de prisma aunque en realidad nisiquiera son poliedros. No obstante su volumen y superficie se obtienen de forma similar.
Halla el área y el volumen de un prisma recto de base triangular, sabiendo que la base es un triángulo rectángulo cuyos catetos miden 3 cm y 4 cm, y la altura mide 9 cm.
Imagina que te contrata una empresa de zumos para que diseñes un nuevo envase. Como el logotipo de la empresa es un hexágono, quieren que la forma del nuevo envase de zumo sea un prisma recto hexagonal. El envase debe caber en las estanterías del supermercado, por lo que te exigen que la altura sea 10 cm. Además quieren que quepa un litro de zumo, es decir, que el volumen del prisma sea 1 litro. ¿Cuánto debe medir el lado de la base?
Ejercicios para calcular el volumen y superficie de distintos prismas.
En esta escena podrás ver el desarrollo de un prisma recto regular y calcular su volumen y sus áreas.
Volumen del ortoedro
Cómo se obtiene el volumen de un ortoedro.
Volumen de un prisma recto (ortoedro) de aristas 12.4, 8.5 y 6.2 cm.
Cálcula el área y el volumen de un prisma cuadrangular regular cuya arista básica mide 6.5 cm, y cuya altura es de 8.4 cm.
Calcula el volumen de una piscina de 50 m de largo, 21 m de ancho y 2 m de alto.
En esta escena podrás ver el desarrollo de un ortoedro y calcular su volumen y su área.
Volumen del cubo
Cálculo del área y volumen de un cubo
Halla el volumen de un cubo cuya superficie total es de 36 cm2.
María tiene una caja para guardar juguetes con forma de cubo cuya arista mide 60 cm. ¿Cuántos m2 de plástico se utilizaron para construirla?. ¿Qué volumen tiene en m3?
Actividades de autoevaluación sobre volúmenes de cubos.
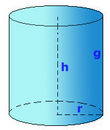
Volumen del cilindro
En esta escena podrás ver el desarrollo de un cilindro y calcular su volumen y sus áreas.
El cilindro:
- Definición.
- Elementos
- Área y volumen.
- Ejercicio.
Cálculo del área total y el volumen de un cilindro. Ejemplos.
Un camión cisterna tiene un depósito cilíndrico de 10 m de largo y bases de 2 m de diámetro. Calcula su capacidad en litros.
Calcula la altura de un cilindro de 825.19 cm3 de volumen y 6 cm de radio de la base.
El área de la base de un cilindro es 25π cm2 y la generatriz es el doble del radio. Halla el volumen.
Ejercicios propuestos
|
Ejercicios propuestos: Volumen del prisma y del cilindro |
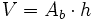
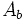 : Área de la base = Área de un polígono.
: Área de la base = Área de un polígono.
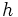 : altura.
: altura.
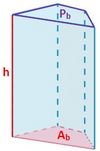
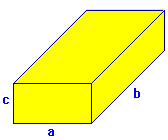
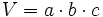
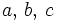 : aristas.
: aristas.
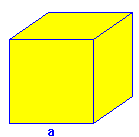
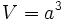
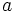 : arista.
: arista.
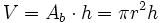
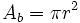
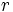 : radio.
: radio.