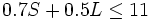Plantilla:Inecuación lineal con dos incógnitas

De Wikipedia

Revisión de fecha 10:16 29 dic 2017; Ver revisión actual
← Revisión anterior | Revisión siguiente →

Saltar a navegación, búsqueda

Una inecuación lineal con dos incógnitas es una inecuación, en la que las expresiones matemáticas que intervienen en la desigualdad, son polinomios de primer grado con dos variables. En consecuencia, puede ponerse, mediante transformaciones, de alguna de estas formas generales:

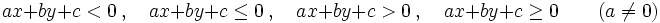
$ax+by+c<0 \ , \quad ax+by+c \le 0 \ , \quad ax+by+c>0 \ , \quad ax+by+c \ge 0 \qquad (a \ne 0)$

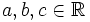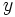donde $a,b,c \in \mathbb{R}$ son los coeficientes y $x \;$ e $y \;$ son las dos variables.

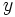Una solución de una inecuación lineal con dos incógnitas, $x\;$ e $y\;$ , es una pareja de valores de las variables, 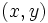$(x,y)\;$ , que hace que se cumpla la desigualdad.

Inecuaciones lineales con dos incógnitas

Tutorial (6´55") Sinopsis:

Definición de inecuación.
Ejemplos de inecuaciones lineales con dos incógnitas.

Ejercicio 1 (6´07") Sinopsis:

Determina si las parejas (3,5) y (1,-7) son soluciones de la inecuación 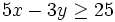$5x-3y \ge 25\;$

Problema 1 (3´08") Sinopsis:

Fabiano quiere lograr al menos 6.5 puntos en un importante torneo de ajedrez. El logra 1 punto por cada partida ganada y 0.5 por cada una empatada. Si llamamos W al número de partidas ganadas y D al número de partidas empatadas, escribe la inecuación que relaciona estas variables con los puntos necesarios para conseguir su objetivo.

Problema 2 (4´45") Sinopsis:

Ezra disfruta de la jardinería. Cada girasol que el riega requiere 0.7 litros de agua y cada azucena requiere 0.5 litros. Ezra tiene un total de 11 litros de agua para estas plantas. En la siguiente desigualdad S representa el número de girasoles y L el número de azucenas que Ezra puede regar:

$0.7S+0.5L \le 11$

Si Ezra riega 10 azucenas, ¿cuántos girasoles podrá regar como máximo con el agua que le sobra?

Problema 3 (5´20") Sinopsis:

Goku quiere tener más de 9000 comentarios en sus videos de YouTube. Él recibe el mismo número de comentarios por cada video de gatos que sube y también el mismo número de comentarios por cada video de perros que sube (aunque el número de comentarios por los videos de perros es distinto que por los de gatos). En la siguiente inecuación, C representa el número de videos de gatos y D el de perros: