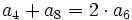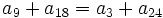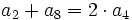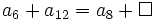Plantilla:Actividades progresiones aritmeticas
De Wikipedia
← Revisión anterior | Revisión siguiente →
|
Actividad: Progresiones aritméticas Dada la sucesión {1, 4, 7, 10, 13, 16, ...}: a) Halla el término general. b) Halla el término 20. c) Halla la suma de los 20 primeros términos. d) Halla la suma de los términos del 8 al 15. d) Halla la suma de los términos del p al q. Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: Tras obtener la solución del apartado a), utilízala para hallas las soluciones de los demás apartados. a) {1, 4, 7, 10, 13, 16, ...} b) {3n-2} for n=20 c) sum {3n-2} for n=1 to 20 d) sum {3n-2} for n=8 to 15 e) sum {3n-2} for n=p to q |
Obtención del término general y de la suma de los términos de la progresión aritmética 1, 6, 11, 16, ...
En una progresión aritmética el primer término es 6 y la diferencia 5. Halla el séptimo término.
En una progresión aritmética el primer término es -6 y el décimo término es 21. Halla la diferencia.
En una progresión aritmética el tercer término es 24 y el décimo término es 66. Halla el primer término y la diferencia.
En una progresión aritmética el segundo término es 20 y el quinto término es 56. Halla el término décimo y la suma de los diez primeros términos.
La suma de los primeros 21 términos de una progresión aritmética es 420. El décimonoveno término es cuatro veces el tercer término. Encuentra el primer término y la diferencia.
Sea 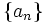 una progresión aritmética de diferencia
una progresión aritmética de diferencia 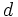 :
:
- Determina
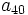 sabiendo que
sabiendo que 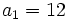 y
y 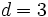 .
.
- Determina
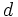 sabiendo que
sabiendo que 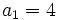 y
y 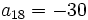 .
.
- Determina
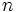 sabiendo que
sabiendo que 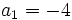 y
y 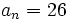 y
y 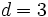 .
.
- Determina
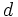 ,
, 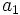 y
y 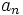 sabiendo que
sabiendo que 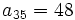 y
y 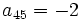 .
.
- Determina
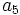 y
y 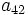 sabiendo que
sabiendo que 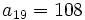 y
y 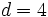 .
.
Sea 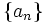 una progresión aritmética. ¿Son ciertas las siguientes afirmaciones?
una progresión aritmética. ¿Son ciertas las siguientes afirmaciones?
Completa las siguientes igualdades:
- Sea
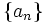 una progresión aritmética. Halla
una progresión aritmética. Halla 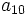 sabiendo que
sabiendo que 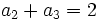 y
y 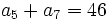 .
.
- Si las longitudes de los lados de un triángulo rectángulo están en progresión aritmética, determina el perímetro sabiendo que la hipotenusa mide 30 m.
- Determina tres números en progresión aritmética de modo que su suma sea 12 y la suma de sus cuadrados sea 16.
- Determina los lados de un triángulo rectángulo sabiendo que están en progresión aritmética de diferencia 7.
Sea 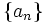 una progresión aritmética de diferencia d. Determina:
una progresión aritmética de diferencia d. Determina:
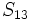 sabiendo que
sabiendo que 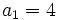 y
y 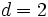 .
.
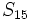 sabiendo que
sabiendo que 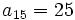 y
y 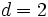 .
.
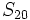 sabiendo que
sabiendo que 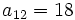 y
y 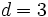 .
.
- k sabiendo que
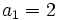 ,
, 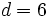 y
y 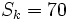 .
.
Sea 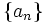 una progresión aritmética de diferencia
una progresión aritmética de diferencia 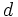 . Determina:
. Determina:
- d sabiendo que
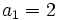 y
y 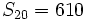
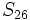 sabiendo que
sabiendo que 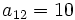 y
y 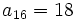 .
.
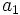 sabiendo que d=3 y
sabiendo que d=3 y 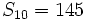 .
.
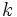 sabiendo que
sabiendo que 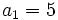 ,
, 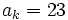 y
y 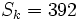 .
.
- La suma de los n primeros términos de la sucesión 3, 7, 11, ... es 210. Halla n.
- La suma de los 6 primeros términos de una progresión aritmética es 36, siendo
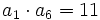 . Determina el término general de la progresión.
. Determina el término general de la progresión.
Halla el término general de una progresión aritmética cuya diferencia es 3 y cuyo quinto término es -1. calcula también la suma de los 20 primeros términos.
En una progresión aritmética se cumple que 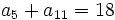 y
y 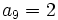 . Halla
. Halla 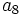 ,
, 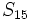 y
y 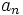 .
.
La suma de los 50 primeros términos de una progresión aritmética es 2650. Si la diferencia es 2, calcula el primer término y los términos centrales.
Ejercicios
Problemas
|
Problema: Progresiones aritméticas Al excavar tierra para hacer un túnel se pagan 700€ por el primer metro y 95€ de aumento por cada metro sucesivo (es decir, 795€ por el segundo metro,...). a) ¿Cuánto se pagará por el décimo metro excavado? b) Calcular el total abonado por los 10 metros excavados.Solución: 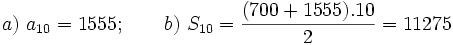 |