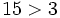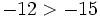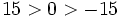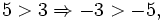Plantilla:Orden en el conjunto de los números reales
De Wikipedia
En el conjunto de los números reales existe un orden que queda constatado al representarlos gráficamente en la recta numérica.
Un número es mayor que otro si está situado más a la derecha en la recta numérica y es menor si está situado más a la izquierda.
Relación de orden
Dados dos números, 
y 
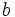, se dará uno de los siguientes casos:
- El primero es menor que el segundo:
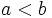(Se lee "a es menor que b").
- El primero es igual que el segundo:
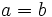(Se lee "a es igual que b").
- El primero es mayor que el segundo:
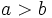(Se lee "a es mayor que b").
Al comparar números, además de los símbolos anteriores, podemos utilizar también los siguientes:
- Menor o igual que (
)
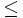- Mayor o igual que (
)
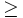- Distinto (
)
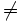Propiedades
- Todo número negativo es menor que cero y todo número positivo es mayor que cero.
- Si dos números son positivos, el mayor es el que tiene mayor valor absoluto.
- Si dos números son negativos, el mayor es el que tiene menor valor absoluto.
- Si , entonces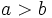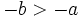
Tutorial 1 (3'32") Sinopsis:Relación de orden en el conjunto de los números reales.
Tutorial 2 (5'09") Sinopsis: Desigualdades.
Ejemplo 1 (7'10") Sinopsis: Representando desigualdades sencillas en la recta numérica.
Ejemplo 2 (4'49") Sinopsis: Problemas verbales de desigualdades.
Ejercicio (1'37") Sinopsis: Representa en la recta numérica los valores de x que cumplen que x < 4.
Actividad 1 Descripción: Representación gráfica de desigualdades en la recta numérica.
Autoevaluación 1 Descripción: Escribir desigualdades numéricas.
Autoevaluación 2 Descripción: Problemas verbales de desigualdades.
Autoevaluación 3 Descripción: Representación gráfica de desigualdades en la recta numérica.
Autoevaluación 4 Descripción: Autoevaluación sobre inecuaciones.
