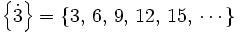Divisibilidad
De Wikipedia
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Relación de divisibilidad
Dos números enteros  y
y 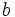 (
(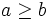 ) , están emparentados por la relación de divisibilidad cuando la división
) , están emparentados por la relación de divisibilidad cuando la división 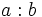 es exacta.
es exacta.
- Un listón de 60 cm se puede partir, exactamente, en trozos de 15 cm, porque la división 60:15 es exacta (cociente=4; resto=0). Por tanto, 60 y 15 están emparentados por la relación de divisibilidad.
- Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 no están emparentados por la relación de divisibilidad.
Actividad de introducción a la relación de divisibilidad.
Múltiplos y divisores
Si  y
y 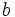
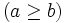 están emparentados por la relación de divisibilidad, es decir,
están emparentados por la relación de divisibilidad, es decir, 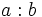 es exacta, entonces decimos que:
es exacta, entonces decimos que:
 es multiplo
es multiplo 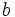 y lo expresaremos simbólicamente:
y lo expresaremos simbólicamente: 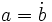 .
.
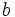 es divisor de
es divisor de  y lo expresaremos simbólicamente:
y lo expresaremos simbólicamente: 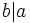 .
.
- La división 60:15=4 es exacta. Entonces 60 es un múltiplo de 15
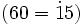 y 15 es un divisor de 60
y 15 es un divisor de 60 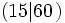 .
.
- Fíjate que 4 también es divisor de 60 porque la división 60:4=15 es también exacta. Por tanto, los divisores siempre van por parejas.
Proposición
Si  es multiplo de
es multiplo de 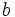 , entonces existe un número entero
, entonces existe un número entero 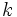 tal que
tal que 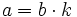 .
.
En efecto, si a es multiplo de b, entonces la división a:b es exacta. Si llamamos k al cociente, se cumple que a=b·k.
¿Cómo se sabe si un número es múltiplo o divisor?
Las definiciones vistas hasta ahora las podríamos haber dado igualmente cambiando números enteros por números naturales. En lo que resta de tema sólo hablaremos de números naturales para evitar duplicidades por cuestiones de signo, sin embargo, todo lo que digamos será también aplicable a números enteros, salvo pequeños matices que obviaremos por cuestiones de simplicidad.
Propiedades
Propiedades de los múltiplos
- Todo número natural es múltiplo de 1 y de sí mismo.
- Todo número natural
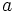 tiene infinitos múltiplos,
tiene infinitos múltiplos, 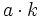 , que se obtienen multiplicándolo por un número natural
, que se obtienen multiplicándolo por un número natural 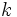 cualquiera.
cualquiera.
- El 0 es múltiplo de cualquier número.
- La suma de dos o más multiplos de
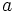 es otro múltiplo de
es otro múltiplo de 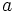 .
.
- La diferencia de dos múltiplos de un número es otro múltiplo de dicho número.
- Si un número es múltiplo de otro, y éste lo es de un tercero, el primero es múltiplo del tercero.
- Si un número es múltiplo de otro, todos los múltiplos del primero lo son también del segundo.
Propiedades de los divisores
- Todo número natural distinto de cero tiene al menos dos divisores: 1 y él mismo.
- Todo divisor de un número distinto de cero es menor o igual a él. Por tanto, el número de divisores es finito.
- Si un número es divisor de otros dos, también lo es de su suma y de su diferencia.
- Si un número es divisor de otro, también lo es de cualquier múltiplo de éste.
- Si un número es divisor de otro, y éste lo es de un tercero, el primero lo es del tercero.
Cálculo de los múltiplos y divisores de un número
Los siguiente videotutoriales condensan todo lo que se va a ver en este apartado.
Múltiplos y divisores de un número. Cómo obtenerlos. Ejemplos.
Tutorial en el que se explica los conceptos matemáticos de múltiplo y divisor y se enseña a como obtener los múltiplos y divisores de números naturales.
- 00:00 a 03:25: Explicación del concepto matemático de múltiplo.
- 3:25 a 06:25: Obtención de los múltiplos de un número natural.
- 6:25 a 09:20: Explicación del concepto matemático de divisor.
- 9:20 a 16:35: Obtención de los divisores de un número natural.
- 6:35 a 17:56: Números primos y compuestos.
Cálculo de los múltiplos y los divisores (requiere factorizción) de un número natural. Ejemplos.
¿Cómo hallar los múltiplos y divisores de un número?
- Conceptos de múltiplo y divisor de un número.
- ¿Cómo hallar los múltiplos y divisores de un número?
Múltiplos y divisores de un número.
Cálculo de los múltiplos de un número
La segunda de las propiedades de los múltiplos vista anteriormente me da una forma de calcular los múltiplos de un número natural.
Procedimiento
Para obtener los múltiplos de un número natural  , multiplicaremos
, multiplicaremos  por cada uno de los números naturales:
por cada uno de los números naturales:
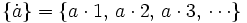
Ejercicio resuelto: Cálculo de los múltiplos de un número
Calcula los múltiplos de 17 comprendidos entre 150 y 200.
Al dividir 150 : 17 obtenemos 8 de cociente y 14 de resto.
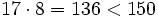
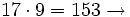 Primer múltiplo de 17 mayor que 150.
Primer múltiplo de 17 mayor que 150.
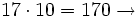 Segundo múltiplo de 17 mayor que 150.
Segundo múltiplo de 17 mayor que 150.
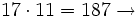 Tercer múltiplo de 17 mayor que 150.
Tercer múltiplo de 17 mayor que 150.
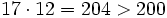 .
.
Qué son y como se obtienen los múltiplos de un número. Ejemplos.
Qué son y como se obtienen los múltiplos de un número. Ejemplos.
Múltiplos de un número entero. Qué son los múltiplos de un número entero, cómo se calculan y como se averigua si un número es múltiplo de otro.
calcula los múltiplo9s de 6 y de 13.
- Actividad para ver algunos múltiplos de un número.
- Actividad en la que deberás separar los números que aparecen según sean múltiplos o no del indicado.
Escribe los cuatro primeros múltiplos de 5, sin contar el cero, ordenados de menor a mayor.
Escribe los cuatro primeros múltiplos de 25, sin contar el cero, ordenados de menor a mayor.
Escribe los cinco primeros múltiplos de 12 mayores que 1000.
Calcula tres múltiplos de 7 comprendidos entre 50 y 100.
Si escribes números cada vez mayores empezando en cero y avanzando de 3 en 3, ¿cuál será el número más cercano, anterior a 400, que alcanzarás?
Marca los números que sean a la vez múltiplos de 3 y de 5.
Ejercicios de autoevaluación sobre múltiplos de un número.
Cálculo de los divisores de un número
Procedimiento
Para encontar todos los divisores de un número, 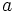 , buscamos las divisiones exactas
, buscamos las divisiones exactas 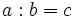 . Entonces
. Entonces 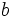 y
y 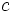 son divisores de
son divisores de 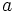 . Para ello procederemos de la siguiente manera:
. Para ello procederemos de la siguiente manera:
- Probaremos con
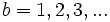 .
.
- Para cada valor de
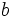 que dé división exacta (
que dé división exacta (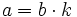 ), tendremos dos divisores:
), tendremos dos divisores: 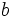 y
y 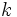 .
.
- Pararemos de probar cuando el cociente de la división
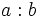 sea menor o igual que
sea menor o igual que 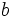 .
.
Ejercicio resuelto: Cálculo de los divisores de un número
Calcula los divisores de 44.
44 : 1 = 44  1 y 44 son divisores. Sigo porque 44 > 1
1 y 44 son divisores. Sigo porque 44 > 1
44 :2 = 22  2 y 22 son divisores. Sigo porque 22 > 2
2 y 22 son divisores. Sigo porque 22 > 2
44 : 3  No es exacta (cociente=14). Sigo porque 14 > 3
No es exacta (cociente=14). Sigo porque 14 > 3
44 : 4 = 11  4 y 11 son divisores. Sigo porque 11 > 4
4 y 11 son divisores. Sigo porque 11 > 4
44 : 5  No es exacta (cociente=8). Sigo porque 8 > 5
No es exacta (cociente=8). Sigo porque 8 > 5
44 : 6  No es exacta (cociente=7). Sigo porque 7 > 6
No es exacta (cociente=7). Sigo porque 7 > 6
44 : 7  No es exacta (cociente=6). Paro porque 6 < 7
No es exacta (cociente=6). Paro porque 6 < 7
Qué son y como se obtienen los divisores de un número. Ejemplos.
En este video podrás ver:
- Divisores de un número.
- Cálculo de los divisores de un número.
Este video también incluye los siguientes contenidos que veremos posteriormente en otro tema:
- Criterios de divisibilidad.
- Números primos y números compuestos.
Calcula los divisores de 50 y de 60.
Calcula los divisores de 120.
¿Cuáles de los siguientes números son divisores de 154?: 3, 5, 6, 9 y 14.
Dos viejos amigos se encuentran y uno de ellos le pregunta al otro:
- ¿Cuántos hijos tienes? - Tres hijas. - ¿Qué edades tienen? - La multiplicación de sus edades es 36 y la suma es igual al número del portal que ves enfrente. - Mmm. Me falta un dato! - Cierto. La mayor toca el piano.
¿Qué edades tienen las hijas?
- Actividad que te muestra todos los divisores de un número dado.
- Actividad en la que debes averiguar todos los divisores de un numero dado.
- Actividad en la que debes separar los divisores de un número de los que no lo son.
Marca en la tabla todos los divisores del número dado.
Actividad en la que deberás hallar los divisores de un número.
Actividad en la que podrás calcular los divisores de un número.
Parejas de divisores de un número.
Nota: En esta actividad se llaman factores a los divisores.
Ejercicios de autoevaluación sobre divisores de un número.
Actividades
Actividades sobre múltiplos y divisores de un número.
Múltiplos y divisores de un número.
Nota: En esta actividad se llaman factores a los divisores.
Múltiplos y divisores de un número.
Nota: En esta actividad se llaman factores a los divisores.
Múltiplos y divisores de un número.
Nota: En esta actividad se llaman factores a los divisores.
Ejercicios de autoevaluación sobre múltiplos y divisores de un número.
|
Actividad: Múltiplos y divisores de un número
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Criterios de divisibilidad
Los siguientes criterios nos permiten averiguar si un número es divisible por otro de una forma sencilla, sin necesidad de realizar una división.
| Divisible por: | Criterio |
|---|---|
| 2 | El número acaba en 0 ó cifra par. |
| 3 | La suma de sus cifras es un múltiplo de 3. |
| 4 | El número formado por las dos últimas cifras es múltiplo de 4. |
| 5 | La última cifra es 0 ó 5. |
| 6 | El número es divisible por 2 y por 3. |
| 7 | La diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es 0 ó un múltiplo de 7. |
| 8 | El número formado por las tres últimas cifras es múltiplo de 8. |
| 9 | La suma de sus cifras es múltiplo de 9. |
| 10 | La última cifra es 0. |
| 11 | Se suman las cifras que forman el número de forma alternativa y se restan los resultados para ver si da un múltiplo de 11 (El cero también lo es) |
Los números que aparecen en verde se corresponden con aquellos cuyo criterio es un proceso que se puede usar de forma recursiva, es decir, si después de aplicarlo no sabemos si el número al que hemos llegado es múltiplo del número en cuestión, podemos aplicar nuevamente el criterio sobre ese resultado.
Criterios de divisibilidad por 2, 3 y 5. Ejemplos.
Criterios para averiguar si un número es divisible por 2, 3, 5, 10 u 11. Ejemplos.
Criterios para averiguar si un número es divisible por 2, 3, 5, 9 u 11. Ejemplos.
Criterios de divisibilidad por 2, 3, 4, 5 y 6. Ejemplos.
Criterios de divisibilidad por 7, 8, 9, 10 y 11. Ejemplos.
Criterios de divisibilidad por 2, 3, 4, 5, 6, 7, 8, 9, 10 y 11. Ejemplos.
Tutorial que explica los criterios de divisibilidad más básicos e importantes, es decir los "trucos" para saber, sin necesidad de dividir, si 2, 3, 5, 7, 11 y 10nson divisores de un número.
- 00:00 a 04:20: Definiciones básicas (divisor).
- 04:20 a 05:55: Criterio de divisibilidad del 2.
- 05:55 a 07:05: Criterio de divisibilidad del 5.
- 07:05 a 09:50: Criterio de divisibilidad de potencias de 10.
- 09:50 a 15:27: Criterio de divisibilidad del 3.
- 15:27 a 21:00: Criterio de divisibilidad del 11.
- 21:00 a 24:50: Criterio de divisibilidad del 7.
Tutorial que explica algunos criterios de divisibilidad más, es decir los "trucos" para saber, sin necesidad de dividir, si 6, 2n, 5n y 9 son divisores de un número.
- 00:00 a 02:20: Definiciones básicas (divisor).
- 02:20 a 05:15: Criterio de divisibilidad de las potencias de 2.
- 05:15 a 07:15: Criterio de divisibilidad de las potencias de 5.
- 07:15 a 10:30: Criterio de divisibilidad del 9.
- 10:30 a 15:46: Criterio de divisibilidad del 6 o producto de primos.
Explicación de por qué funciona el criterio de divisibilidad por 3.
Explicación de por qué funciona el criterio de divisibilidad por 9.
Criterios de divisibilidad por 2
Criterios de divisibilidad por 3
Criterios de divisibilidad por 4
Criterios de divisibilidad por 5
Criterios de divisibilidad por 9
Criterios de divisibilidad por 10
Criterios de divisibilidad por 11
Comprueba si son divisibles por 2, 3, 4, 5, 6, 10, 11 ó 12, los siguientes números: 405, 316, 814, 3080 y 240.
Escribe cuatro números de forma que sean divisibles a la vez entre 2 y 11.
Comprueba si son divisibles por 2, 3, 4, 5, 6, 9 ó 10, los siguientes números: 2 799 588, 5670 y 100 765.
Comprueba si 380 es divisible por 2, 3, 4, 5, 6, 9 ó 10.
- Actividad en la que podrás comprobar si un número dado es múltiplo o no de 2, 3, 4, 5, 6, 8, 9, 10 y 11.
- Actividad en la que deberás separar los números por los que es divisible un número dado.
Actividad sobre criterios de divisibilidad por 2, 3, 5, 7, 9, 10 y 11.
Averigua los múltiplos de 2
Averigua los múltiplos de 3
Averigua los múltiplos de 5
Averigua los múltiplos de 11
Averigua qué número no es múltiplo del dado.
Test de 5 preguntas sobre divisibilidad.
Test de 5 preguntas sobre divisibilidad.
Test de 7 preguntas sobre divisibilidad.
- Criterios de divisibilidad del 2, 3, 5 y 11
Ejercicios de autoevaluación sobre criterios de divisibilidad.
Números compuestos y números primos
Propiedad
Conceptos de número primo y número compuesto. Tabla de números primos menores que 100. Conceptos de número primo y número compuesto. Conceptos de número primo y número compuesto. Breve explicación de qué son los números primos, cómo reconocerlos y cómo encontrarlos fácilmente Conceptos de número primo y número compuesto. Criba de Eratóstenes. Números primos. The building blocks of all natural numbers are the prime numbers. The early Greeks invented the system still used today for separating natural numbers into prime and composite numbers. (Disponibles los subtítulos en inglés) Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado) Determina cuáles de los siguientes números son primos, cuáles son compuestos, y cuáles no son ni primos ni compuestos: 24, 2, 1 y 17. |
- Actividad en la que puedes ver si un número es primo o compuesto.
- Actividad en la que debes separar los números primos de los compuestos.
Introducción a los números primos y compuestos.
Repaso sobre números primos y compuestos.
Actividad en la que aprenderás a determinar si un número es primo o compuesto.
Actividad en la que deberás decidir si un número es primo o compuesto.
Actividad en la que deberás decidir si un número es primo o compuesto.
Actividad en la que deberás pulsar sobre los números primos.
Identifica números primos.
Identifica números compuestos.
Test de 10 preguntas sobre números primos y compuestos.
Ejercicios de autoevaluación sobre números primos.
Ejercicios de autoevaluación sobre números compuestos.
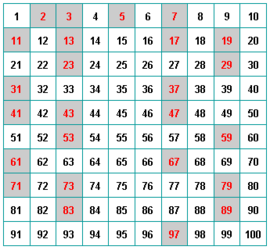
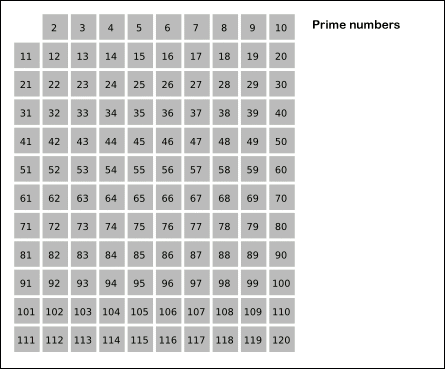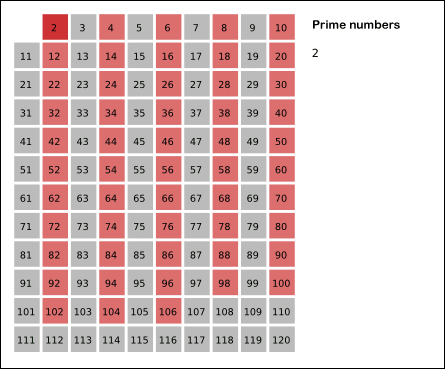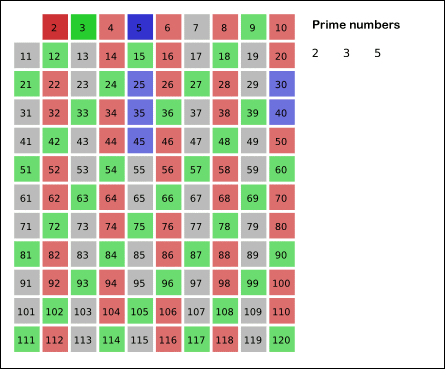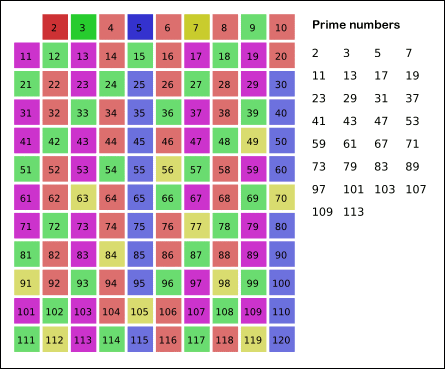
Criba de Eratóstenes
La criba de Eratóstenes es un algoritmo que permite hallar todos los números primos menores que un número natural dado n, que desarrolló el célebre matemático griego Eratóstenes en el siglo III a.C. Procedimiento Se forma una tabla con todos los números naturales comprendidos entre 2 y n, y se van tachando los números que no son primos de la siguiente manera:
|
Determinemos, mediante el siguiente ejemplo, el proceso para determinar la lista de los números primos menores de 20.
- Primer paso: listar los números naturales comprendidos entre 2 y 20.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
- 2. Segundo paso: Se toma el primer número no rayado ni marcado, como número primo.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
- 3. Tercer paso: Se tachan todos los múltiplos del número que se acaba de indicar como primo.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
- 4. Cuarto paso: Si el cuadrado del primer número que no ha sido rayado ni marcado es inferior a 20, entonces se repite el segundo paso. Si no, el algoritmo termina, y todos los enteros no tachados son declarados primos.
- Como 3² = 9 < 20, se vuelve al segundo paso:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
- 5. Quinto paso: En el cuarto paso, el primer número que no ha sido tachado ni marcado es 5. Se tachan sus múltiplos. Como su cuadrado es mayor que 20, el algoritmo termina y se consideran primos todos los números que no han sido tachados.
- Como resultado se obtienen los números primos comprendidos entre 2 y 20, y estos son: 2, 3, 5, 7, 11, 13, 17, 19.
Determinación de los números primos utilizando la Criba de Eratóstenes.
Al seguir este método de búsqueda de primos, cada vez que marcamos un número como primo, no es necesario empezar a buscar sus múltiplos desde el más pequeño, sino desde su cuadrado, pues todos los anteriores ya habrían sido eliminados por ser múltiplos de primos más pequeños.
En esta escena podrás practicar el procedimiento de la criba de Eratóstenes para obtener números primos.
Actividad para practicar la criba de Eratóstenes.
Cómo averiguar si un número es primo
Procedimiento para ver si un número es primo
Para averiguar si un número es primo, efectuamos divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que la división sea exacta (entonces no es primo) o el cociente sea menor o igual que el siguiente número primo por el que toca dividir (entonces es primo).
Ejemplo: Averiguar si un número es primo
Averigua si el número 167 es primo.
Efectuamos las siguientes divisiones por los distintos números primos: 2, 3, 5, 7, 11, 13, 17,... hasta que sea divisible o el cociente sea menor o igual que el siguiente número primo por el que toca dividir:
- 167 : 2
 (cociente=83, resto=1) No es divisible por 2. Como 83>3 sigo probando con 3.
(cociente=83, resto=1) No es divisible por 2. Como 83>3 sigo probando con 3.
- 167 : 3
 (cociente=55, resto=2) No es divisible por 3. Como 55>5 sigo probando con 5.
(cociente=55, resto=2) No es divisible por 3. Como 55>5 sigo probando con 5.
- 167 : 5
 (cociente=33, resto=2) No es divisible por 5. Como 33>7 sigo probando con 7.
(cociente=33, resto=2) No es divisible por 5. Como 33>7 sigo probando con 7.
- 167 : 7
 (cociente=23, resto=6) No es divisible por 7. Como 23>11 sigo probando con 11.
(cociente=23, resto=6) No es divisible por 7. Como 23>11 sigo probando con 11.
- 167 : 11
 (cociente=15, resto=2) No es divisible por 11. Como 15>13 sigo probando con 13.
(cociente=15, resto=2) No es divisible por 11. Como 15>13 sigo probando con 13.
- 167 : 13
 (cociente=12, resto=11) No es divisible por 13. Como 12<17 paro.
(cociente=12, resto=11) No es divisible por 13. Como 12<17 paro.
- Números primos y compuestos.
- Averigua si son primos o compuestos los siguientes números: 263, 137 y 119.
Averigua si son primos o compuestos los siguientes números: 43, 293 y 611.
Descomposición factorial de un número
Se le llama descomposición factorial o factorización de un número, a su expresión como producto de potencias de números primos.
Descomposición en factores primos
Cualquier número puede expresarse como producto de potencias de números primos.
El procedimiento es el siguiente:
- Lo dividimos por el menor número primo que podamos.
- El cociente que haya resultado lo colocamos debajo del número.
- Si podemos, seguimos dividiendo sucesivamente ese cociente por el mismo número primo.
- Cuando no podamos hacer la división por ese número primo, lo hacemos por el siguiente primo que se pueda.
- Así sucesivamente hasta que el cociente final sea 1.
- El producto de todos los números primos por los que hemos ido dividiendo constituyen la descomposición factorial del número.
Halla la descomposición factorial de 90.
Solución:
Dividimos 90 entre el primer número primo por el que sea divisible. En este caso, por 2. (90:2=45) A continuación, procedemos a dividir 45, cociente de la anterior división, de igual forma. (45:3=15) Así sucesivamente hasta obtener 1 en el cociente (15:3=5; 5:5=1)
Los cocientes 2, 3, 3 y 5 son los factores que descomponen a 90.
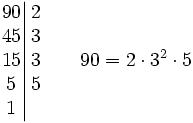
Descomposición factorial de un número. Ejemplos
Tutorial que explica la factorización de números en factores primos. Se explican dos técnicas para realizarlo, la técnica de columna que es el método más habitual que se enseña en casi todas las escuelas y la técnica del árbol, un método muy secillo, rápido y que permite poderlo hacer mentalmente después de práctica.
- 00:00 a 03:10: Definiciones básicas.
- 03:10 a 16:32: Método de columna.
- 16:32 a 27:28: Método de árbol.
Descomposición factorial de un número. Ejemplos
Descomposición factorial de un número mediante árbol de factores.
Descomposición factorial de un número.
Descomposición factorial de un número.
Descomposición factorial de un número por el método tradicional y el de árbol.
Descompón en factores primos: 18, 56 y 693
Descompón en factores primos: 30
Descompón en factores primos: 99
Descompón en factores primos: 18, 70, 132 y 480
Descompón en factores primos: 12, 9 y 108
Descompón en factores primos: 1176, 825 y 364
Descompón en factores primos el número 75.
Descompón en factores primos: 95, 85 y 5.
- Actividad en la que puedes ver la descomposición factorial de un número dado.
- Actividad para practicar la descomposición en factores primos de un número dado
Descomposición factorial de un número.
Descomposición factorial de un número.
Máximo común divisor
El máximo común divisor (m.c.d.) de dos o más números es el mayor de todos los divisores comunes a esos números.
Propiedades
- Si
 es múltiplo de
es múltiplo de 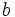 , entonces
, entonces 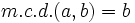 .
.
- Los divisores comunes de varios números coinciden con los divisores del m.c.d.
- Dados varios números, si se multiplican o dividen por otro número, entonces su m.c.d también queda multiplicado o dividido por el mismo número.
- Dados dos números naturales,
 y
y 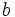 , se cumple:
, se cumple:
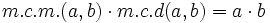
- Un ejemplo de la primera propiedad:
- m.c.d.(15, 30) = 15, porque 30 es múltiplo de 15.
- Un ejemplo de la última propiedad:
- m.c.d.(6,20) = 2 y m.c.m.(6,20) = 60
- m.c.m.(6,20) · m.c.d.(6,20) = 2 · 60 = 120
- a · b = 6 · 20 = 120.
Cálculo del máximo común divisor
Ya sabemos encontrar todos los divisores de un número. Ahora nos interesa hallar un divisor en concreto. Queremos, de entre todos los divisores comunes a varios enteros, el mayor de ellos.
Y, ¿por qué el mayor?, ¿por qué un divisor común a varios números?, ¿para qué sirve esto?. Lo cierto es que el cálculo del máximo común divisor será muy útil para resolver problemas de divisibilidad en los que intervengan varios números. De ahí lo de común y lo de divisor. ¿Y por qué el mayor y no, por ejemplo, el menor? Piensa detenidamente... ¿Qué número es divisor de cualquier entero?. Efectivamente, el 1. ¿Crees que hay divisores menores que 1?
Una primera solución para encontrar el máximo común divisor de varios números podría ser calcular los divisores de cada uno de ellos y comprobar cuál es el mayor de los divisores comunes. A este método lo llamaremos "método artesanal".
Procedimiento artesanal
Para calcular el máximo común divisor de dos o más números se siguen los siguientes pasos:
- Averiguaremos todos los divisores de dichos números.
- De los divisores comunes (los que se repitan en todos) cogeremos el mayor.
Calcula el m.c.d.(24,60) por el método artesanal
- Divisores de 24: 1, 2, 3, 4, 6, 8, 12, 24
- Divisores de 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
- m.c.d.(24,60)= 12
Problemas prácticos en los que calcularemos el m.c.d. por el método artesanal.
Calcula:
- a) m.c.d. (12, 8)
- b) m.c.d. (25, 20)
- c) m.c.d. (5, 12)
- d) m.c.d. (6, 12)
Calcula el m.c.d. (-12, -30) hallando los divisores comunes.
Calcula hallando los divisores comunes:
- a) m.c.d. (6, -12)
- b) m.c.d. (-12, -15)
- c) m.c.d. (-6, 8)
- d) m.c.d. (0, -18)
- e) m.c.d. (6, 4)
- f) m.c.d. (8, -72)
Calcula hallando los divisores comunes:
- a) m.c.d.(4, 16, 14)
- b) m.c.d.(9, 12, 18)
- c) m.c.d.(8, 16, 28)
- d) m.c.d.(21, 27, 30)
Actividad en la que podrás obtener el m.c.d. de dos números por el método artesanal.
Actividad en la que podrás ver como se obtiene el m.c.d de dos números mediante el procedimiento artesanal.
Pero el método artesanal no es adecuado para números grandes pues requeriría muchos cálculos. Hay otro método basado en la factorización que es mucho más rápido. Lo llamaremos "método óptimo".
Sabemos que los divisores de un número son una combinación de algunos de sus factores primos. Por tanto, si queremos un divisor común a varios números, tendremos que tomar factores primos comunes a todos ellos. Si además queremos que sea el mayor de todos los divisores comunes, tendremos que tomar todos los factores que sean comunes.
Procedimiento óptimo
Para obtener el m.c.d. de dos o más números se siguen los siguientes pasos:
- Se descomponen los números en factores primos.
- Se toman los factores comunes con menor exponente.
- Se multiplican dichos factores y el resultado obtenido es el m.c.d.
En el caso de que no haya ningún factor común, en realidad nos estamos olvidando del 1, que aunque no es primo, es factor de cualquier número entero. Por tanto, si no hay coincidencia de ningún factor primo, el máximo común divisor es 1.
Calcula el m.c.d.(24,60) por el método óptimo
- Descomponemos 24 y 60 en sus factores primos:
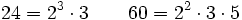
- Multiplicando los factores comunes elevados al menor exponente:
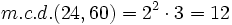
Calcula el m.c.d.(17,19) por el método óptimo
- Descomponemos 17 y 19 en sus factores primos (incluimos al 1 aunque no sea primo):

- El único factor común es 1:
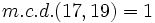
Tutorial que explica el significado del máximo común divisor, es decir "¿qué es?" y las distintas técnicas para su cálculo, desde mentalmente o bien obteniendo los divisores de los números, para el caso de número pequeños, o el algoritmo general.
- 00:00 a 07:33: ¿Qué es el máximo común divisor? Método de extracción de divisores.
- 07:33 a 13:46: Método general para calcular el m.c.d. Ejemplos.
Tutorial que explica qué es y cómo se calcula el máximo común divisor de dos o tres números.
Concepto y cálculo del máximo común divisor de dos o más números.
Concepto de máximo común divisor. Ejemplo.
Tutorial que explica qué es y cómo se calcula el máximo común divisor de dos números. Desarrolla un ejemplo en el que calcula el m.c.d. mediante el método artesanal.
Cálcula el máximo común divisor de 12 y 20
Cálcula el máximo común divisor de:
a) 12 y 18
b) 360 y 84
c) 40, 72 y 300
Cálcula el máximo común divisor de:
a) 30 y 45
b) 36, 84 y 120
Cálcula el máximo común divisor de:
a) 18 y 24
b) 36, 54 y 90
Calcula:
- a) m.c.d.(36, 48).
- b) m.c.d.(60, 90, 150).
Calcula:
- a) m.c.d.(15, 20)
- b) m.c.d.(12, 18)
- c) m.c.d.(16, 20, 24)
- d) m.c.d.(18, 27)
Calcula:
- a) m.c.d.(8, 20)
- b) m.c.d.(96, 160, 24)
Calcula: m.c.d.(48, 36, 84).
Calcula: m.c.d.(72, 108, 60).
3) Escribe los divisores de 4 y los divisores de 8.
- a) ¿Es 4 divisor de 8?
- b) ¿Son todos los divisores de 4 también divisores de 8?
- c) ¿Es 8 divisor de 4?
- d) ¿Son todos los divisores de 8 también divisores de 4?
- e) ¿Cuál es el m.c.d. de 4 y 8?
Calcula:
- a) m.c.d (16, 8)
- b) m.c.d (40, 45)
- c) m.c.d (9, 6)
- d) m.c.d.(105, 30)
- Actividad en la que podrás obtener el m.c.d. de dos números por descomposición factorial.
- Actividad en la que deberás obtener el m.c.d. de dos números por descomposición factorial.
Actividades sobre el máximo común divisor.
Juego para practicar el m.c.d.
Ejercicios de autoevaluación sobre el m.c.d.
Ejercicios de autoevaluación sobre el m.c.d.
Ejercicios de autoevaluación sobre el m.c.d. (Nivel avanzado)
Algoritmo de Euclides
Proposición
Sean  y
y 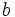 ,
, 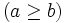 , dos números naturales, entonces se cumple que:
, dos números naturales, entonces se cumple que:
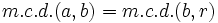
donde 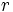 es el resto de la división de
es el resto de la división de  entre
entre 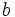 .
.
Apoyándonos en el resultado anterior tenemos el siguiente algoritmo para el cáculo del m.c.d. de dos números.
Algoritmo de Euclides
El algoritmo de Euclides es un procedimiento para calcular el m.c.d. de dos números. Los pasos son:
Se divide el número mayor entre el menor.
- Si la división es exacta, el divisor es el m.c.d.
- Si la división no es exacta, dividimos el divisor entre el resto obtenido y se continúa de esta forma hasta obtener una división exacta, siendo el último divisor el m.c.d.
Cálculo del m.c.d. usando el algoritmo de Euclides.
- Euclides.
- Ejemlplos de cálculo del m.c.d. usando el algoritmo de Euclides.
Cálculo del m.c.d. y del m.c.m. usando el algoritmo de Euclides.
Calcula el m.c.d. de 364 y 748 usando el algoritmo de Euclides.
Calcula el m.c.d. de 136 y 48 usando el algoritmo de Euclides.
Calcula el m.c.d. de 44 y 24 usando el método artesanal y el algoritmo de Euclides.
Calcula el m.c.d. de 100 y 150 usando el método artesanal y el algoritmo de Euclides.
Ejercicios de autoevaluación sobre el algoritmo de Euclides.
Números primos entre sí
Dos o más números son primos entre sí o coprimos, si su m.c.d. es 1, es decir, no tienen divisores comunes salvo la unidad.
- 6 y 11 son primos entre sí ya que no tienen divisores comunes salvo el 1.
- 6 y 27 no son primos entre sí porque tienen como divisor común a 3.
¿Cuándo son dos números primos entre sí?. Ejemplo.
Comprueba si los números 3 y 7 son o no primos entre sí.
Comprueba si los números 11 y 22 son o no primos entre sí.
Comprueba si los números 9 y 48 son o no primos entre sí.
Comprueba si los números 45 y 34 son o no primos entre sí.
Comprueba si los números 6, 8 y 20 son o no primos entre sí.
Propiedades
- Si a y b son primos entre sí, entonces m.c.m.(a,b)=a · b.
- Si se dividen varios números por su m.c.d., los cocientes resultantes son primos entre sí.
- Como 6 y 11 son primos entre sí, entonces m.c.m(6,11)=6·11=66
- Sean los números 1 y 25. Su m.c.d.(10,25)=5
- 10:5=2 y 25:5=5; m.c.d.(2,5)=1, luego 2 y 5 son primos entre sí.
Actividades
Problema resuelto: m.c.d.
En un almacén quieren envasar, para su distribución, 200 kg de manzanas y 260 kg de de naranjas, en cajones del mismo peso y de la mayor carga que sea posible. ¿Cuántos kilos deben poner en cada cajón?
Solucuión: 20 kg
Iker ha cocinado 24 galletas de chocolate, 16 de manzana y 20 buñuelos. Quiere colocarlo todo en platos que contengan un solo tipo de postre y con el mismo número de unidades. Si quiere utilizar el menos número de platos posible, ¿cómo debe hacerlo?.
Se desea dividir un terreno rectangular cuyas dimensiones son de 186 m y 162 m, en parcelas cuadradas, para lo cual se colocan estacas en cada uno de los vértices de las parcelas. ¿Cuántas estacas se necesitarán colocar en total como mínimo?
En una bodega hay 3 toneles de vino, cuyas capacidades son 250, 360 y 540 litros. Se quiere envasar todo el vino en botellas iguales lo más grandes posible. Calcula la capacidad de estas botellas y cuántas serán necesarias.
Un comerciante tiene dos barriles llenos de vino: uno de vino tinto, cuya capacidad es de 250 litros, y otro de vino moscatel, de 160 litros. Para efectos de comercialización y transporte requiere distribuir todo el vino de ambos barriles, sin mezclar los contenidos, en recipientes de igual capacidad, de modo que el número de estos sea el menor posible y estén completamente llenos. ¿Qué cantidad de estos recipientes necesitará para el vino moscatel?
Tres cables que miden 20, 150 y 180 metros se dividen en el menor número de trozos de igual longitud. ¿Cuál es la longitud de cada trozo?
A) 5 m; B) 20 m; C) 12 m; D) 15 m; E) 10 m
Un albañil debe colocar losetas cuadradas en un piso de un baño cuyas dimensiones son 270 cm y 300 cm. ¿Cuántas losetas enteras entrarán en dicho piso, si estas deben ser del mayor tamaño posible?
A) 30; B) 90; C) 10; D) 19
Las edades de dos amigos son como 4 es a 7. Si el mínimo común múltiplo de sus edades es 168 y su máximo común divisor es 6, ¿Cuáles son sus edades?
A) 24 y 48; B) 24 y 36; C) 12 y 24; D) 24 y 42
Camila tiene 24 bocadillos y 20 zumos para repartir en bolsas. Cada bolsa tiene que tener el mismo número de bocadillos y el mismo número de zumos. ¿Cuántas bolsas, como máximo, necesita? ¿Cuántos zumos y cuántos bocadillos mete en cada bolsa?
Nivel más avanzado:
Si tienes que llenar 4 cilindros de capacidades 72, 24, 56 y 120 galones respectivamente. ¿Cuál es la capacidad del balde que puede usarse para llenarlos exactamente si está comprendida entre 2 y 8 galones?
Juan tiene un terreno de forma rectangular de 40m de ancho y 96m de largo. si se divide su terreno en parcelas cuadradas iguales y planta en el interior de cada parcela 3 árboles, ¿cuál es el mínimo número de árboles que podría sembrar en todo su terreno?
a) 160; b) 150; c) 190; d) 170; e) 180
Raúl compró cierto número de televisores por S/.31500 y vendió unos cuantos en S/15000, cobrando cada televisor lo mismo que le había costado. ¿Cuántos televisores le quedan si el precio de estos es el mayor posible?
a) 11; b) 9; c) 13; d) 10; e) 12
Se desea colocar postes igualmente espaciados en el perímetro de un terreno rectangular de 280 m de largo por 120 m de ancho. Si se sabe que debe colocarse un poste en cada esquina y el número de postes debe ser el menor posible, determínese el número total de postes por colocar.
A) 24; B) 20; C) 48; D) 40; E) 18
Un comerciante desea poner en cajas 6690 manzanas y 6630 naranjas, de modo que cada caja contenga el mismo número de piezas de fruta, y además, el mayor número posible. Halla el número de piezas de fruta de cada caja.
¿Cuántos centímetros mide el lado de la mayor baldosa que cabe un número exacto de veces en una sala de 20 m de largo y 16 m de ancho?
Mínimo común múltiplo
El mínimo común múltiplo (m.c.m.) de dos o más números, es el menor de todos los múltiplos comunes a esos números, distinto de cero.
Propiedad
- Si a es múltiplo de b, entonces
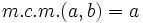 .
.
- Los múltiplos comunes de varios números son también múltiplos del m.c.m.
- Cualquier múltiplo del m.c.m. de varios números también lo es de dichos números.
- Dados varios números, si se multiplican o dividen por otro número entonces su m.c.m también queda dividido o multiplicado por el mismo número.
Cálculo del mínimo común múltiplo
Nos preguntamos a continuación por los múltiplos comunes de dos o más números? ¿Nos interesa encontrar el mayor o el menor? ¿Será útil?.
En el caso de los múltiplos, nos interesará encontrar el común más pequeño. No tiene sentido preguntarse por el mayor, pues hay infinitos múltiplos comunes a varios números. Una vez encontrado el más pequeño, se pueden conseguir tantos como quieras, sólo tienes que multiplicarlo por cualquier número natural.
Una posible estrategia sería buscar múltiplos de los números por separado hasta que lleguemos a encontrar el primero que sea igual para todos. A este procedimiento lo llamaremos 2método artesanal".
Procedimiento artesanal
Para calcular el mínimo común múltiplo de dos o más números obtendremos los múltiplos de dichos números y seleccionaremos el primero que se repita en todos ellos.
Calcula el m.c.m.(24,60) por el método artesanal:
- Múltiplos de 24: 24, 48, 72, 96, 120, 144,...
- Múltiplos de 60: 60, 120, 180, ...
- m.c.m.(24,60)= 120
Problemas prácticos en los que calcularemos el m.c.m. por el método artesanal.
1) Dados los números del 1 al 20:
- a) Rodea de rojo los múltiplos de 3 y de azul los de 6.
- b) ¿Cuáles son múltiplos comunes de 3 y 6?
- c) ¿Cuál es el m.c.m. de 3 y 6?
2) Calcula hallando los múltiplos comunes:
- a) m.c.m.(3, 5)
- b) m.c.m.(4, 5)
- c) m.c.m.(3, 7)
- d) m.c.m.(4, 6)
- e) m.c.m.(3, 9)
3) Calcula hallando los múltiplos comunes:
- a) m.c.m.(10, 20, 8)
- b) m.c.m.(2, 4, 5)
- c) m.c.m.(3, 4, 6)
Calcula m.c.m.(15, 6, 10)
Actividad en la que podrás obtener el m.c.m. de dos números por el método artesanal.
El método artesanal es lento y puede llegar a exigir escribir mucho. No es un buen método para números grandes. A continuación presentamos un método mejor, que llamaremos "método óptimo", y que se apoya en la factorización.
Sabemos que cada múltiplo de un número entero contiene a todos los factores primos de dicho número. Entonces, lo lógico sería coger todos los factores que aparezcan en las descomposiciones de los números con los que trabajemos. Lógicamente, si hay factores repetidos, los escogeremos una sola vez, ya que queremos que nuestro múltiplo común sea el menor de todos los que hay.
Procedimiento óptimo
Para obtener el m.c.m. de dos o más números se siguen los siguientes pasos:
- Se descomponen los números en factores primos.
- Se toman los factores comunes y no comunes con mayor exponente.
- Se multiplican dichos factores y el resultado obtenido es el m.c.m.
Calcula el m.c.m.(24,60) por el método óptimo:
- Descomponemos 24 y 60 en sus factores primos:
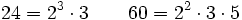
- Multiplicando todos los factores elevados al mayor exponente:
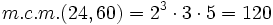
Tutorial que explica el significado del mínimo común múltiplo con un simpático ejemplo.
Tutorial que explica el significado del mínimo común múltiplo, es decir "¿qué es?" y las distintas técnicas para su cálculo, desde mentalmente o bien obteniendo los múltiplos de los números, para el caso de número pequeños, o el algoritmo general.
- 00:00 a 06:33: ¿Qué es el Mínimo Común Múltiplo? Método de extracción de múltiplos.
- 06:33 a 11:18: Método general para calcular el MCM. Ejemplos.
Tutorial que explica qué es y cómo se calcula el mínimo común múltiplo de dos o tres números.
Mínimo común múltiplo de dos números enteros. Ejemplo.
Tutorial que explica qué es y cómo se calcula el mínimo común múltiplo de dos números. Desarrolla un ejemplo en el que calcula el m.c.m. mediante el método artesanal.
Cálcula el mínimo común múltiplo de:
a) 12 y 18
b) 360 y 84
c) 40, 72 y 300
Cálcula el mínimo común múltiplo de:
a) 4 y 3
b) 4 y 30
c) 75, 25 y 15
d) 98, 10 y 45
Cálcula el mínimo común múltiplo de:
a) 6 y 8
b) 14, 21 y 28
Cálcula el mínimo común múltiplo de:
a) 4 y 6
b) 9, 10 y 15
Calcula el mínimo común múltiplo de 28 y 21 por el método artesanal y el método óptimo.
Calcula:
- m.c.m.(6, 8)
- m.c.m.(2, 4, 10)
- m.c.m.(10, 15)
- m.c.m.(2, 5, 30)
Calcula:
- m.c.m.(4, 10)
- m.c.m.(8, 14, 20)
Calcula: m.c.m.(72, 108).
Calcula: m.c.d.(336, 540).
Calcula: m.c.d.(12, 9, 108).
Calcula:
- a) m.c.m.(20, 2)
- b) m.c.m.(24, 18)
Calcula m.c.m.(20, 18)
- Actividad en la que podrás obtener el m.c.m. de dos números por descomposición factorial.
- Actividad en la que deberás obtener el m.c.m. de dos números por descomposición factorial.
- Actividad en la que deberás obtener el m.c.m. de tres números por descomposición factorial.
Actividades sobre cómo se calcula el mínimo común múltiplo.
Cálculo del mínimo común múltiplo de dos números
Ejercicios de cálculo del mínimo común múltiplo de dos números
Ejercicios de autoevaluación sobre el m.c.m.
Actividades
Problema resuelto: m.c.m.
Un distribuidor de electrodomésticos desea cargar dos palés, uno con lavavajillas de 45 kg y otro con frigoríficos de 40 kg, de forma que ambos pesen lo mismo y lo menos posible. ¿Cuánto pesará cada palé?
Solución: 360 Kg
María tarda 6 min en dar una vuelta al barrio corriendo y Pedro 8 min. ¿Cuándo coincidirán de nuevo en la plaza si han salido juntos de ella a las 10:15?
Un viajero va a Brasil cada 18 días y otro cada 24. Si hoy han estado los dos en Brasil, ¿cuántos días pasarán para que vuelvan a coincidir?
Necesitamos hacer bolsitas con 3 caramelos de los colores de las luces de un semáforo (rojo, verde y amarillo). En la tienda donde venden los caramelos me dicen que los caramelos rojos vienen en paquetes de 6, los amarillos en paquetes de 5 y los verdes en paquetes de 10. ¿Cuántos paquetes, como mínimo, tenemos que usar para hacer bolsitas con cada uno de los tres colores sin que nos sobre ninguno?.¿Cuántas bolsitas nos saldrán?
Cuatro ciclistas compiten en una pista circular y la recorren totalmente en 8, 10, 12 y 15 segundos, respectivamente. Si parten juntos, ¿en cuantos minutos se encontraran en la partida?
A) 120; B) 1; C) 2; D) 3
De los 630 primeros números enteros positivos, ¿cuántos son múltiplos de 3 y 7 a la vez?
A) 10; B) 21; C) 20; D) 30
El número de páginas de un libro está comprendido entre 300 y 350. Si se cuentan de 3 en 3, sobran 2; de 4 en 4 sobran 3 y de 7 en 7 sobran 6. ¿Cuántas páginas tiene el libro?
A) 325; B) 345; C) 315; D) 335
Claudia va al hospital cada 15 días, Joaquín cada 12 y Ángel cada 18. Si hoy es 05 de Septiembre y se encontraron en el hospital, entonces la fecha más próxima en la cual se encontrarán los tres nuevamente será:
A) 5 de Enero; B) 5 de Diciembre; C) 4 de Marzo; D) 4 de Febrero; E) 2 de Marzo
Antonio va al piscina cada 6 días y Alba cada 4 días. ¿Cuántos días, pasarán para que vuelvan a coincidir por primera vez? ¿Qué día de la semana será?
Nivel más avanzado:
Se compran televisores de 17 pulgadas a 3 por 1200 dólares y se venden a 4 por 2400 dólares. Para ganar 3000 dólares, ¿cuántos se debe vender?
A) 12; B) 15; C) 14; D) 8; E) 10
Un vendedor tiene entre 600 y 800 naranjas. Si se puede agruparlas de 15 en 15, de 18 en 18 y de 24 en 24 sin que sobre alguna, ¿cuántas naranjas tiene el vendedor?
A) 640; B) 6800; C) 720; D) 760; E) 800
Se tiene tres reglas calibradas, de 48 cm cada una. La primera está calibrada con divisiones de 4/21 cm; la segunda, con divisiones de 24/35 cm; y la tercera, con divisiones de 8/7 cm. Si se hace coincidir las tres reglas en sus extremos de calibración, ¿cuántas coincidencias de calibración hay en las tres reglas?
A) 13; B) 14; C) 4; D) 15; E) 12
Marina tiene una planta que riega cada 3 días y otra que riega cada 5. Si el lunes ha regado las dos, ¿qué día de la semana volverá a regar otra vez las dos?
En una parada de autobús comienzan dos líneas. Los autobuses de una línea salen cada 6 minutos, y los de la otra, cada 8. Si dos autobuses de distintas líneas salen a la misma hora, ¿Cuántos minutos tardarán en volver a coincidir en la salida?
Un faro se enciende cada 12 segundos, otro cada 18 segundos, y un tercero cada minuto. A las 6:30 de la tarde los tres coinciden. Averigua las veces que volverán a coincidir durante los próximos 5 minutos.
Tres ciclistas tardan en dar la vuelta a un velódromo 48, 56 y 72 segundos, respectivamente. Si salen a la vez, ¿al cabo de cuántos segundos volverán a coincidir en la salida?
Ejercicios y problemas
Actividades sobre divisibilidad.
Ejercicios de repaso del tema de divisibilidad.
Ejercicios resueltos sobre divisibilidad.
Autoevaluación del tema de divisibilidad.
Autoevaluación sobre divisibilidad.
Test sobre divisibilidad.
Test de 20 preguntas sobre m.c.d. y m.c.m.
Amplia tus conocimientos sobre divisibilidad.
Control para enviar a tu profesor por correo.
Divisibilidad:
3 problemas en los que debes deducir si se trata de encontrar divisores, múltiplos, si hay que hallar el m.c.m. o el m.c.d. de varios números.
Autoevaluación sobre problemas sobre divisibilidad, incluidos de m.c.d. y m.c.m.
Problemas resueltos sobre divisibilidad, incluidos de m.c.d. y m.c.m.
M.c.d. y m.c.m.:
Autoevaluación sobre problemas de m.c.d. y m.c.m.
Autoevaluación sobre problemas de m.c.d. y m.c.m.
- Pedro va a visitar a sus abuelos cada 12 días, su hermano va cad 20 y su hermana cada 8. Si hoy coinciden los tres en casa de sus abuelos, ¿cuándo coincidirán nuevamente?
- Un zoo desea trasladar 90 gacelas y 64 leones en jaulas con el mismo número de animales y del mayor tamaño posible. ¿Cuántos animales irán en cada jaula?
- Para transportar 12 perros y 18 gatos se van a usar jaulas iguales que sean lo más grandes posible, de forma que en todas quepa el mismo número de animales. ¿Cuántos animales deben ir en cada jaula?. ¿Cuántas jaulas habrá?
- En un almacén disponemos de 48 botellas de zumo de naranja y otras 72 de zumo de piña. Queremos encargar cajas iguales para guardar ambos zumos en las que quepan el mismo número de botellas. ¿Cuántas botellas habrá en cada caja?
- Dos autobuses salen a la vez de la estación. Uno de ellos completa su recorrido y vuelve cada 36 min, y el otro cada 24. ¿Dentro de cuánto tiempo volverán a coincidir en el punto de salida?
- En mi barrio, el camión que recoge los envases de plástico viene cada 3 días, el que recoge el papel para reciclar, cada 8 días, y el que recoge las pilas usadas, cada 2 semanas. Si hoy han coincidido los tres camiones, dentro de cuántos días volverán a coincidir?
- Una parcela rectangular mide 60 m de ancho y 45 m de largo. Queremos dividirla en cuadrados lo más grandes posible. ¿Qué dimensiones tendrán los cuadrados?. ¿Cuántos cuadrados habrá?
- Máximo común divisor y mínimo común múltiplo. Conceptos y métodos de cálculo.
- Problemas:
- Elena desea donar a unos niños 18 cuadernos, 24 libros y 36 lapiceros, de tal modo que cada uno reciba la misma cantidad de cada tipo de útiles escolares. ¿Cuál es el mayor número de niños que puede beneficiarse y cuántos útiles de cada tipo recibe cada uno?
- En una competición automovilística de circuito cerrado, tres automóviles parten juntos. Si tardan 10, 12 y 15 minutos en dar una vuelta completa, respectivamente, ¿al cabo de cuanto tiempo pasarán juntos por la línea de partida?
- Carlos y Daniel están en clases distintas de Física e la Universidad de Santa Rita. El profesor de Carlos siempre pone exámenes con 30 preguntas, mientras que el profesor de Daniel siempre los pone de 24 preguntas. Si antes de empezar el curso ambos profesores acordaron realizar la misma cantidad de preguntas en el transcurso del curso, ¿Cuál es el mínimo número de preguntas que deberán poner a lo largo del curso y cuál es el mínimo número de exámenes que tendría que poner cada profesor?
- Elena compró un paquete de 21 carpetas y un paquete de 30 lápices. Si ella quiere usar todo el material para crear juegos idénticos de material de oficina para su compañera de clase, ¿Cuál es el número máximo de conjuntos idénticos que puede hacer usando este material?
|
Problemas: m.c.d y m.c.m.
1. Cierto planeta A tarda 150 días en completar una orbita completa alrededor de su sol. Otro planeta B del mismo sistema solar lo hace en 225 días. Si cierto día ambos planetas están alineados con el sol, ¿Cuánto tardarán en volver a estarlo?
Solución: 450 años.
2. Jaime hace una revisión rutinaria de su vehículo cada 15.000 km y hace otra revisión más a fondo cada 70.000 km ¿Cada cuántos kilómetros coinciden las dos revisiones?
Solución: 210.000 km.
3. Una empresa vinícola de Montilla tiene que embasar 1.650 litros de vino dulce y 3.600 litros de vino fino, en toneles iguales de la mayor capacidad posible. ¿De qué capacidad serán los toneles?
Solución: 150 l.
4. Se desea cubrir con azulejos cuadrados una pared de una cocina que mide 210 cm de ancho por 300 cm de alto. Si queremos que los azulejos sean lo más grande posible y que no haya que romper ninguno, ¿cuál debe ser la anchura del azulejo?
Solución: 30 cm.
5. En una peña hay entre 300 y 400 amigos. Para hacer una competición podemos formar grupos de 9, de 15 o de 21, sin que sobre o falte nadie. ¿Cuántos son en la peña?
Solución: 315
6. Si agrupamos las cajas de una almacén de 2 en 2, de 3 en 3, o de 4 en 4, siempre sobra 1. Calcula cuántos cajas hay sabiendo que no hay más de 20.
Solución: 13 |