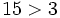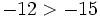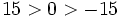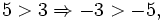Números enteros: Definición
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Sistemas numeración | Naturales Enteros | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
Estamos acostumbrados a utilizar números en multitud de ocasiones. Al levantarnos vemos la hora en el despertador, al calentar algo en la cocina puede que aparezca marcada la potencia con un entero, el precio de cualquier cosa que compremos está marcada con números, ...
En muchas situaciones utilizamos incluso valores negativos: "Pulsa el -1 para bajar al primer sótano", "¡Qué frío hace hoy! El termómetro marca 5º bajo cero (-5º)".
Los primeros en usar números negativos fueron los chinos, que utilizaban ábacos con varillas de distintos colores para diferenciar los positivos de los negativos. En Europa, sin embargo, fue más difícil su aceptación y grandes matemáticos como Descartes o Cardano se referían a los negativos como "números falsos". A partir del siglo XVIII y gracias al trabajo, entre otros, de Euler, su uso se universalizó y se convirtieron en parte esencial de las matemáticas.
- Introducción histórica de los números negativos.
- SOS, Estoy en números rojos.
- Cuadrados mágicos.
Números naturales
Empezaremos recordando primero qué eran los números naturales.
El conjunto de los números naturales es:
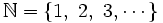
Se trata de un conjunto con infinitos elementos y sirven para:
- Contar (números cardinales: 1, 2, 3, ...).
- Ordenar (números ordinales: 1º, 2º, 3º, ...).
- Identificar y diferenciar los distintos elementos de un conjunto.
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en la prueba de cien metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
El conjunto de los números naturales: origen y definición.
El conjunto de los números naturales: origen y definición.
Tutorial de introducción al tema:
- Números naturales.
- Sistemas de numeración.
- Sistema de numeración decimal.
Hace unas horas tenía 16 años y el año que viene cumpliré 19. ¿Cómo explicas esta situación?
Ejercicios de autoevaluación sobre números naturales.
Existen dos teorías sobre el origen de la numeración, que además está relacionada con la cuestión de qué números aparecieron primero, los cardinales (1, 2, 3,...) o los ordinales (1º, 2º, 3º,...) La teoría que genera más consenso defiende el argumento de la necesidad. Todo habría comenzado a causa de la necesidad de contar objetos; por ello se habrían creado primero los números cardinales y después, los ordinales.
La otra teoría defiende la base espiritual de los números, que habrían tenido un uso ritual: cierto tipo de ceremonias requerían que los participantes se desplazaran o se situaran en un orden ritual preestablecido; por eso los números ordinales serían anteriores a los cardinales. Esta teoría además postula que los números se originaron en un lugar geográfico determinado, desde el que se propagaron al resto del mundo; también establece la división de los números naturales en pares e impares, considerando los impares masculinos y los pares, femeninos, una clasificación que comparten hoy en día muchas culturas del planeta.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 10)"
Véanse los artículos de la BBC:
- ¿Sabes que el 1 y el 2 no son del mismo género y que los números tienen personalidades?
- Lo que quizás no sabías de los números
Representación de los números naturales
Podemos representarlos en una recta:
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado)
Para más información: Números naturales
Números negativos y positivos
- Los números negativos son los números menores que cero. Para representarlos se les pone un signo menos (-) delante:
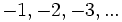
- Los números positivos, son los mayores que cero. Pueden ir precedidos de un signo más (+), pero es habitual no ponerlo:
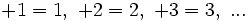
Reglas:
- Los números negativos se escriben precedidos del signo menos (-).
- Si un número lleva signo + o no lleva signo entenderemos que es positivo.
- En las operaciones, los números negativos se escriben entre paréntesis cuando queremos evitar que aparezcan dos símbolos de operación seguidos.
Los números enteros pueden tener signo + (positivos) o signo - (negativos). En este video veremos cuando son necesarios los signos y cuando no. También veremos como se representan en la recta numérica.
Utilidad de los números negativos y positivos
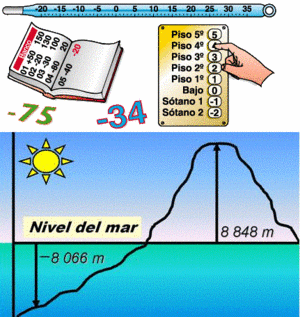
Los números positivos nos sirven para expresar muchas situaciones de la vida cotidiana. Sin embargo, no siempre nos sirven para representar situaciones contrarias que requieren del uso de números negativos, como un saldo deudor en una cuenta bancaria, una temperatura bajo cero, el número de una planta del sótano de un edificio, etc.
Interpretar números negativos. Los números negativos y positivos, además de servir para representar cantidades fijas, también se pueden utilizar para expresar variaciones que sufre una magnitud. Ejemplo: Expresa numéricamente cada enunciado:
Solución: Solución:
|
Utilidad de los números negativos en la vida real.
Números enteros
Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor hay que restarle uno mayor. Nos vemos obligados a ampliar el concepto de números naturales, introduciendo un nuevo conjunto numérico llamado números enteros.
El conjunto de los números enteros
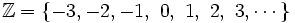
Está formado por:
- El conjunto de los números naturales o enteros positivos :
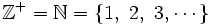 .
.
- Sus opuestos, los enteros negativos:
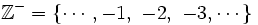 .
.
- El cero (0).
Como consecuencia, 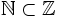 , que se lee: "el conjunto de los números naturales está incluido en el conjunto de los números enteros".
, que se lee: "el conjunto de los números naturales está incluido en el conjunto de los números enteros".
Los números enteros: utilidad y definición.
Los números enteros: utilidad y definición.
En este video vamos a ver lo que son los números enteros y también las clases de números enteros que hay, es decir, números enteros positivos y números enteros negativos, además del cero.
El conjunto de los números enteros. El subconjunto de los números enteros positivos, el de los negativos y el cero. Representación y notación.
El conjunto de los números enteros. Utilidad. Representación y operaciones en la recta numérica.
Las criaturas o entes llamados números no exixten realmente: nadie ha visto jamás un número, ya sea famoso (como el representado por el símolo 5 y llamado cinco) o no. Los números sólo exixten a la luz de la inteligencia humana. Existen en la medida en que nos son útiles. Los Números Naturales son todos enteros y positivos. Son muy útiles para contar, pero tienen sus limitaciones, de manera que hubo que inventar otro tipo de números...
Number systems evolved from the natural "counting" numbers, to whole numbers (with the addition of zero), to integers (with the addition of negative numbers), and beyond. These number systems are easily understood using the number line.
(Disponibles los subtítulos en inglés)
Utilidad de números negativos en la vida real. El conjunto de los números enteros. Representación en la recta numérica.
Los números enteros son infinitos y, al igual que los números naturales sirven para contar. Sin embargo, los números enteros permiten expresar cantidades negativas como un saldo deudor en una cuenta bancaria, un año de la era antes de Cristo, el número de una planta del sótano de un edificio, etc.
Actividad sobre números enteros.
El termómetro y los números enteros.
Actividades sobre números enteros.
Representación de los números enteros
Representación de los números enteros
Los números enteros podemos representarlos en una recta:
- Sobre ella marcamos el número cero.
- A la derecha del cero, y a distancias iguales, se van señalando los números positivos: 1, 2, 3, ...
- A la izquierda del cero, y a distancias iguales que las anteriores, se van señalando los números negativos: −1, −2, −3, ...
- Escena en la que vas a conocer como se representan los números enteros en la recta numérica.
- Actividad en la que debes averiguar el número entero que se corresponde con un punto dado de la recta numérica.
Los números negativos en la recta numérica.
En este video vamos a ver como se representan gráficamente los números enteros sobre la recta numérica y algunos ejemplos.
Introducción a los números negativos. Representación en la recta numérica.
Representa en la recta numérica -4 y 7, e indica cuántos números enteros hay entre ellos.
|
Actividad: Números enteros. Representación
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Valor absoluto de un entero
El valor absoluto de un número entero  se representa por
se representa por 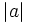 y se define de la siguiente manera:
y se define de la siguiente manera:
- Si el número es positivo, su valor absoluto es él mismo.
- Si el número es negativo, su valor absoluto es igual a su opuesto.
Propiedades
- El valor absoluto de un número es la distancia que lo separa del cero en la recta numérica.
- El valor absoluto de un número siempre es positivo o cero.
- El valor absoluto de cero es cero.
Valor absoluto de un número entero. Interpretación métrica.
- Representación de los números enteros en la recta real.
- Valor absoluto de un número entero. Interpretación métrica.
Valor absoluto de un número entero. Ejemplos.
Valor absoluto de un número entero. Ejemplos.
Valor absoluto de un número entero. Ejemplos.
En este video vamos a ver lo que es el valor absoluto de un número entero y también vamos a aprender a calcularlo.
Valor absoluto de un entero.
Valor absoluto como distancia entre números.
Halla 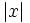 , cuando
, cuando 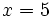 ,
, 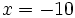 y
y 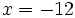 .
.
Compara:
- a)
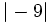 y
y 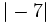
- b)
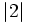 y
y 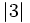
- c)
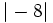 y
y 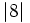
- d)
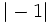 y
y 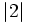 .
.
Ordena de menor a mayor: 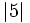 ,
, 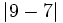 ,
, 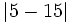 ,
, 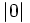 y
y 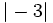 .
.
- Actividad en la que puedes obtener el valor absoluto de un número entero.
- Actividad en la que deberás obtener el valor absoluto de un número entero.
Aprende a pensar el valor absoluto como la distancia a cero, y practica encontrar valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Halla el valor absoluto.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Compara valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Cálculo de distancias mediante valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Opuesto de un entero
El opuesto de un número entero, 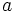 , es otro número entero,
, es otro número entero, 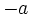 , simétrico de
, simétrico de 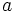 respecto del cero. En consecuencia, se encuentra a la misma distancia del cero que
respecto del cero. En consecuencia, se encuentra a la misma distancia del cero que 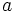 , pero tiene signo contrario. Lo escribiremos
, pero tiene signo contrario. Lo escribiremos 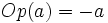 .
.
Es obvio que si 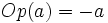 entonces
entonces 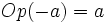 , y viceversa. Por eso, también se dice que
, y viceversa. Por eso, también se dice que  y
y 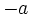 son números opuestos.
son números opuestos.
Concepto de opuesto de un número entero. Ejemplos.
Concepto de opuesto de un número entero. Ejemplos.
Opuesto de un número entero. Representación en la recta numérica.
Uso del signo "menos" para la obtención del opuesto de un número entero.
Ejercicios sobre números opuestos.
- Actividad en la que podrás ver la relación entre un número y su opuesto mediante su representación en la recta real.
- Actividad en la que deberás obtener el opuesto de un número entero.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
|
Actividad: Opuesto de un número entero
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Orden en el conjunto de los enteros
En la representación de los números enteros en la recta numérica se observa el orden que existe en dicho conjunto.
Un número es mayor que otro si está situado más a la derecha en la recta numérica y es menor si está situado más a la izquierda.
Relación de orden
Dados dos números,  y
y 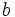 , se dará uno de los siguientes casos:
, se dará uno de los siguientes casos:
- El primero es menor que el segundo:
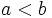 (Se lee "a es menor que b").
(Se lee "a es menor que b").
- El primero es igual que el segundo:
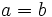 (Se lee "a es igual que b").
(Se lee "a es igual que b").
- El primero es mayor que el segundo:
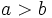 (Se lee "a es mayor que b").
(Se lee "a es mayor que b").
Al comparar números, además de los símbolos anteriores, podemos utilizar también los siguientes:
- Menor o igual que (
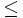 )
)
- Mayor o igual que (
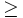 )
)
- Distinto (
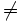 )
)
Propiedades
- Todo número negativo es menor que cero y todo número positivo es mayor que cero.
- Si dos números son positivos, el mayor es el que tiene mayor valor absoluto.
- Si dos números son negativos, el mayor es el que tiene menor valor absoluto.
- Si
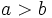 , entonces
, entonces 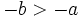
Representación y ordenación de números enteros.
Hacer una comparación de números enteros significa conocer cuál de esos números es mayor (o menor que el otro). Una forma de saberlo es haciendo la representación gráfica de esos números enteros sobre la recta. Los números situados más hacia la derecha en la recta siempre son mayores que los situados a su izquierda.
Ordenando números negativos.
Comprueba gráficamente que 5 > -5.
Comprueba gráficamente que -6 > -1.
Escribe y representa todos los números enteros más grandes que -1 y más pequeños que +5.
Escribe y representa en la recta numérica todos los números comprendidos entre -5 y 1.
Escribe y representa en la recta numérica todos los números enteros más grandes que -3 y más pequeños que 3.
Escribe un valor correcto para x e y que cumplan x < 8 < y.
Ordena de menor a mayor: 5, -3, 0, 4, -6, +1, -1, 3, -7, +6
En una estación meteorológica al sur de Argentina se realizó una medición de la temperatura en el transcurso del día, obteniendo los siguientes resultados: -10º, -3º, 12º, 1º, -8º, -5º, 4º. Ordénalos.
- Actividad en la que puedes ver como se ordenan dos números enteros comparando su posición en la recta numérica.
- Actividad para ordenar dos números enteros.
- Actividad para ordenar varios números enteros.
Ordenar números enteros.
Ordenar números enteros.
Ejercicios de autoevaluación sobre el orden en el conjunto de los números enteros.
|
Actividad: Orden en el conjunto de los números enteros
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Actividades
Repaso del tema de números enteros.
Ejercicios de autoevaluación sobre números enteros.
Actividad en la que podrás comprobar tus conocimientos sobre números enteros.
Ejercicios de autoevaluación sobre números enteros y valor absoluto.
Actividad en la que podrás comprobar tus conocimientos sobre el opuesto y el valor absoluto de un número.


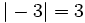
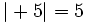
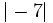
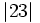
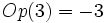 (El opuesto de 3 es -3).
(El opuesto de 3 es -3).
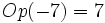 (El opuesto de -7 es 7).
(El opuesto de -7 es 7).
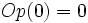 (El opuesto de 0 es 0).
(El opuesto de 0 es 0).