Plantilla:Actividades progresiones geometricas
De Wikipedia
Actividad: Progresiones geométricas Dada la sucesión {1, 1/2, 1/4, 1/8, ...}: a) Halla el término general. b) Halla el término 10. c) Halla el producto de los 10 primeros términos. d) Halla la suma de los términos del 10 al 15. e) Halla la suma de los infinitos términos. Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: Tras obtener la solución del apartado a), utilízala para hallas las soluciones de los demás apartados. a) {1, 1/2, 1/4, 1/8, ...} b) {2^(-n+1)} for n=10 c) product {2^(-n+1)} for n=1 to 10 d) sum {2^(-n+1)} for n=10 to 15 d) sum {2^(-n+1)} for n=1 to oo
|
Ejercicio 1 (13'04") Sinopsis: Obtención del término general y de la suma de los términos de las siguientes progresiones geométricas:
- a) Dada la progresión 2, 6, 18, 54, ..., halla su término general y la suma de los 20 primeros términos.
- b) Dada la progresión 8, 4, 2, 1, ... , halla su término general y la suma de todos sus términos.
Ejercicio 2 (4'16") Sinopsis: El primer término de una progresión geométrica es 3 y la razón 2. Halla el quinto término y la suma de los ocho primeros términos.
Ejercicio 3 (4'59") Sinopsis: El primer término de una progresión geométrica es -4 y el sexto término es 972. Halla la razón.
Ejercicio 4 (9'55") Sinopsis: El cuarto término de una progresión geométrica es 8 y el noveno término es 1/4. Halla la suma de todos los términos de la progresión.
Ejercicio 5 (4'17") Sinopsis: Determina tres números en progresión geométrica de manera que su producto sea 216 y su suma 19.
Ejercicio 6 (6'04") Sinopsis: - Determina la progresión geométrica tal que
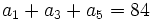y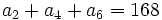 
.
- Determina tres números en progresión geométrica de manera que su suma sea 28 y la diferencia entre el tercero y el primero sea 12.
Ejercicio 7 (7'27") Sinopsis: Determina tres números en progresión geométrica de manera que al sumar 2 al segundo resulta una progresión aritmética, y al sumar 9 al tercero de ésta última resulta una progresión geométrica.
Ejercicio 8 (8´14") Sinopsis: Sea {an} una progresión geométrica de razón r. Determina:
-
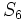sabiendo que 
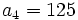y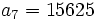 
-
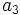sabiendo que r=2 y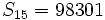 
- n sabiendo que
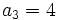, r=2 y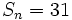 
Ejercicio 9 (3´22") Sinopsis: Resuelve la ecuación: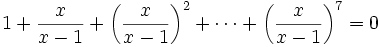 
Ejercicio 10: Capitalización compuesta (6´42") Sinopsis: Fórmula para la obtención del capital final en un sistema de capitalización o interés compuesto como aplicación de las progresiones geométricas.
Ejercicio 11: Capitalización compuesta (6´22") Sinopsis: - Determina el montante obtenido al invertir 1500 € durante 5 años al 9% de interés compuesto anual.
- Determina el capital C que debe invertirse durante 4 años al 7% de interés compuesto anual para obtener un montante de 3000 €.
- Si el montante obtenido al cabo de 5 años por un capital de 1350 € es de 1702.57 €, calcula el tipo de interés compuesto anual.
- Si el interés compuesto anual es del 5%, calcula el tiempo que ha estado invertido un capital de 2100 € si el montante obtenido es de 2954.91 €
Ejercicio 12: Fondo de pensiones (5´39") Sinopsis: Fórmula para la obtención del capital final en un sistema de pensiones basado en un sistema de capitalización compuesta como aplicación de las progresiones geométricas.
Ejercicio 13: Amortización de un préstamo (6´35") Sinopsis: Fórmula para la obtención de la anualidad que hay que pagar al final de cada año para amortizar un préstamo a un cierto interés.
Ejercicio 14 (4´04") Sinopsis:En una progresión geométrica de razón 3, el cuarto término vale 13. Halla el término general.
Ejercicio 15 (5´31") Sinopsis:En una progresión geométrica de razón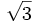 
, el tercer término vale 
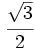. Halla el sexto término y la suma de los seis primeros términos.
Ejercicio 16 (12´14") Sinopsis:Ejercicios.
