Tartaglia
De Wikipedia
Niccolò Fontana (1500 - 1557), matemático italiano apodado Tartaglia (el tartamudo) desde que de niño recibió una herida en la toma de su ciudad natal, Brescia, por parte de los franceses.
Tabla de contenidos |
Vida
Huérfano y sin medios materiales para proveerse una instrucción, llegó a ser uno de los principales matemáticos del siglo XVI. Explicó esta ciencia sucesivamente en Verona, Vicenza, Brescia y finalmente Venecia, ciudad en la que falleció en 1557 en la misma pobreza que le acompañó toda su vida. Se cuenta que Tartaglia sólo aprendió la mitad del alfabeto de un tutor privado antes de que el dinero se agotara, y posteriormente tuvo que aprender el resto por su cuenta. Sea como sea, su aprendizaje fue esencialmente autodidacta.
Niccolò Fontana era el hijo de Michele Fontana. En 1505, Michele fue asesinado, y Niccolò, sus dos hermanos y su madre cayeron en la pobreza. Niccolò experimentó su mayor tragedia en 1512 cuando los franceses invadieron Brescia durante la Guerra de la Liga de Cambrai. La milicia de Brescia defendió su ciudad durante siete días. Cuando el francés rompió las defensas finalmente, se tomaron la revancha y masacraron a los habitantes de Brescia. Al final de la batalla, más de 45.000 residentes fueron asesinados. Durante la matanza, un soldado francés cortó la mandíbula de Niccolò. Esto hizo imposible que Niccolò pudiese hablar normalmente, impulsando el apodo de "Tartaglia (tartamudo).
Él y sus contemporáneos, trabajando fuera de las academias, fueron los responsables de la difusión de obras clásicas en las lenguas modernas entre la clase media educada.
Obra
Matemáticas
Descubridor de un método para resolver ecuaciones de tercer grado, estando ya en Venecia, en 1535 su colega Antonio del Fiore, discípulo de Scipione del Ferro, de quien había recibido la fórmula para resolver las ecuaciones cúbicas, le propone un duelo matemático que Tartaglia acepta. A partir de este duelo y en su afán de ganarlo Tartaglia desarrolla la fórmula general para resolver las ecuaciones de tercer grado. Por lo que, consigue resolver todas las cuestiones que le plantea su contrincante, sin que éste logre resolver ninguna de las propuestas por Tartaglia.
El éxito de Tartaglia en el duelo llega a oídos de Cardano que le ruega que le comunique su fórmula, a lo que accede pero exigiéndole a Cardano jurar que no la publicará. Sin embargo, en vista de que Tarataglia no publica su fórmula, y que según parece llega a manos de Cardano un escrito inédito de otro matemático fechado con anterioridad al de Tartaglia y en el que independiente se llega al mismo resultado, será finalmente Cardano quien, considerándose libre del juramento, la publique en su obra Ars Magna (1570). A pesar de que Cardano acreditó la autoría de Tartaglia, éste quedó profundamente afectado, llegando a insultar públicamente a Cardano tanto personal como profesionalmente. Las fórmulas de Tartaglia serían conocidas como fórmulas de Cardano.
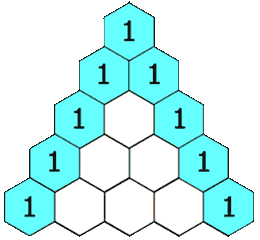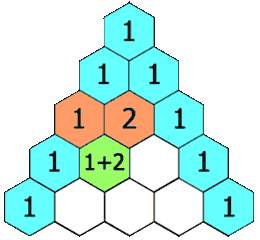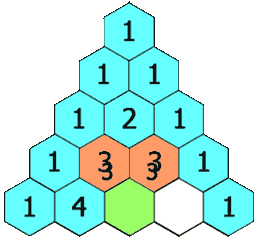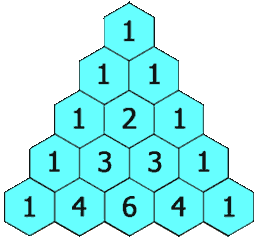
Triángulo de Tartaglia
Tartaglia es también conocido por su método para obtener coeficientes binomiales: El Triángulo de Tartaglia (también llamado Triángulo de Pascal)
Fórmula de Tartaglia
Es una expresión matemática para el cálculo del volumen de un tetraedro cualquiera en función de las longitudes de sus lados. Se trata de una generalización de la fórmula de Herón para el cálculo del área del triángulo:
La Fórmula de Tartaglia dice que el volumen de un tetraedro viene dado por:
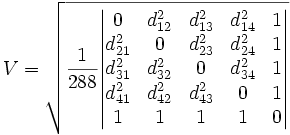
donde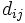 
son las distancias entre los vértices 
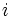y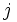 
del tetraedro.
Otras aportaciones
Otras aportaciones destacables de Tartaglia fueron los primeros estudios de aplicación de las matemáticas a la artillería en el cálculo de la trayectorias de los proyectiles (trabajos confirmados posteriormente por los estudios acerca de la caída de los cuerpos realizados por Galileo)
Además de sus trabajos matemáticos, Tartaglia publicó las primeras traducciones al italiano de las obras de Arquímedes y Euclides. Su edición de Euclides en 1543, la primera traducción de los Elementos a un idioma europeo moderno, fue especialmente significativo. Durante dos siglos Euclides se había enseñado a partir de dos traducciones latinas tomadas de una fuente árabe, que contenías errores en el Libro V, la teoría eudoxiana de la proporción, que la hacía inutilizable. La edición de Tartaglia se basó en la traducción latina de Zamberti de un texto en lengua griega incorrupto, y dictó el Libro V correctamente. También escribió el primer comentario moderno y útil sobre la teoría. Más tarde, la teoría fue un instrumento esencial para Galileo, tal como lo había sido para Arquímedes.
Obras
- "Trattato di numeri et misure"
- "Nuova Scientia, cioè invenzione nuovamente trovata utile per ciascuno speculativo matemático bombardero et altri", (1546)
- "Quesiti et invenzioni diverse"
- "La travagliata invenzione"
- "Trattato di aritmetica"
