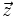Vectores: Definición y operaciones (1ºBach)
De Wikipedia
| Revisión de 17:20 8 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:43 9 oct 2016 Coordinador (Discusión | contribuciones) (→Vectores equipolentes. Vectores libres) Ir a siguiente diferencia → |
||
| Línea 45: | Línea 45: | ||
| }} | }} | ||
| }} | }} | ||
| - | {{p}} | + | {{p}}{{p}} |
| - | {{AI_enlace | + | {{Geogebra_enlace |
| - | |titulo1=Actividad 1: ''Módulo, dirección y sentido de un vector fijo'' | + | |descripcion=En esta escena podrás ver un conjunto de vectores equipolentes. |
| - | |descripcion=En la escena puedes ver varios vectores fijos. | + | |enlace=[https://ggbm.at/YF5N7HbP Vectores equipolentes] |
| - | + | ||
| - | #¿Cuáles de ellos crees que tienen la misma dirección? (Para comprobarlo puedes pulsar el botón azul del "control" rectas.) | + | |
| - | #De los que tienen la misma dirección ¿cuáles tienen el mismo sentido? | + | |
| - | #Te parece que hay vectores en la escena con el mismo módulo? | + | |
| - | + | ||
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores1_1.html | + | |
| - | width=430 | + | |
| - | height=390 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | |url1=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores1_1.html | + | |
| }} | }} | ||
| - | {{p}} | ||
| - | {{AI_enlace | ||
| - | |titulo1=Actividad 2: Vectores equipolentes | ||
| - | |descripcion=Dos vectores fijos son equipolentes si tienen el mismo módulo, dirección y sentido. Para comprobarlo, se unen sus orígenes y sus extremos respectivos. Si el polígono resultante es un paralelogramo, los vectores son equipolentes. | ||
| - | |||
| - | #Comprueba si los vectores <math>\overrightarrow{AB}</math> y <math>\overrightarrow{CD}</math> son equipolentes. Para ello pincha y arrastra los puntitos amarillos que ves en A y B. | ||
| - | #Comprueba si los vectores <math>\overrightarrow{EF}</math> y <math>\overrightarrow{GH}</math> son equipolentes. | ||
| - | #Dibuja en tu cuaderno dos vectores que sean equipolentes y otros dos que no lo sean, dibujando , para demostrarlo, los polígonos correspondientes | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores1_2.html | ||
| - | width=430 | ||
| - | height=390 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores1_2.html | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{AI_enlace | ||
| - | |titulo1=Actividad 3: Vectores libres | ||
| - | |descripcion=Encierra en cada caja los vectores que te parezcan equipolentes al que ya está dentro. (Para ello pincha y arrastra el puntito negro que ves en el origen de cada vector. Puedes usar el zoom si lo necesitas.) | ||
| - | |||
| - | ¿Cuántos vectores libres se obtienen? | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores1_3.html | ||
| - | width=540 | ||
| - | height=440 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/descartes/m_Geometria/vectores/vectores1_3.html | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:43 9 oct 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 172)
Vectores
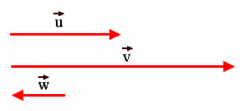
Vectores fijos
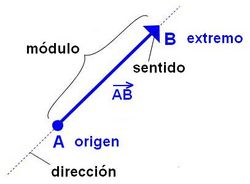
Un vector fijo es un segmento orientado que queda determinado por un punto origen, A y otro punto extremo, B. Lo simbolizamos Características de un vector:
|
Vector nulo
El vector nulo es aquel cuyo origen y extremo coinciden y, por tanto, tiene módulo cero. Lo simbolizaremos 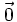 .
.
Vectores opuestos
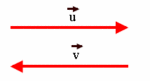
Dos vectores, |
Vectores equipolentes. Vectores libres
Dos vectores, Dado un vector, existen infinitos vectores equipolentes a él. Cuando queremos hacer uso de un vector podemos elegir uno de esos infinitos vectores iguales a él y utilizarlo como representante del vector. Al conjunto de todos los vectores equipolentes a uno dado se le llama vector libre. Un vector libre lo denotaremos mediante una letra con una flecha: |
En esta escena podrás ver un conjunto de vectores equipolentes.
}}
Operaciones con vectores
Producto de un vector por un número
El producto de un número real
En esta escena podrás ver como se multiplica un vector por un número o escalar. |
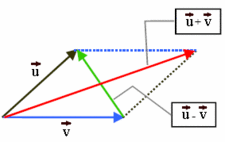
Suma y resta de vectores
| Suma de vectores:
Dados dos vectores En esta escena podrás ver como se suman vectores por dos métodos geométricos. |
| Resta de vectores:
Para restar dos vectores |
| Método del paralelogramo:
Si consideramos el paralelogramo que resulta de los vectores En esta escena podrás ver como se suman y restan vectores. |
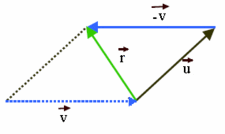
Combinación lineal de vectores
Dados dos vectores En el gráfigo de la derecha tenemos un ejemplo en el que el vector La definición anterior se puede extender a mas de dos vectores, así, por ejemplo, el vector 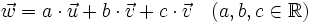 es combinación lineal de En esta escena podrás ver como se expresa un vector como combinación lineal de otros dos. |
Cómo expresar gráficamente un vector como combinación lineal de otros dos
Procedimiento
Para expresar gráficamente el vector 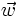 como combinación lineal de los vectores
como combinación lineal de los vectores 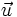 y
y 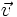
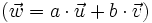
- Colocamos los tres vectores partiendo de un mismo punto.
- A continuación, por el extremo de
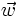 trazamos paralelas a los otros dos vectores.
trazamos paralelas a los otros dos vectores.
- Donde estas paralelas corten a las prolongaciones de los vectores, tenemos los extremos del vector
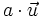 y
y 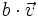 .
.
En esta escena podrás ver como se expresa gráficamente un vector como combinación lineal de otros dos.
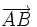
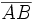
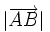
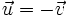
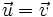
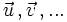
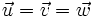
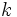 por un vector
por un vector 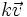
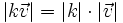
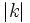 es el valor absoluto del número real
es el valor absoluto del número real 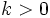 y opuesto si
y opuesto si 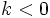 .
.
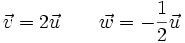
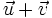
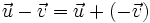 .
.
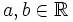 , el vector
, el vector 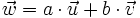 se dice que es una combinación lineal de
se dice que es una combinación lineal de 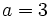 y
y 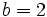 .
.