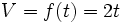Plantilla:Formas de expresar una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:09 12 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | Hay varias formas de expresar una función: | + | Una función se puede expresar de varias formas: |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| * Mediante un '''enunciado''' que explique la relación que existe entre las variables. | * Mediante un '''enunciado''' que explique la relación que existe entre las variables. | ||
| * Mediante una '''expresión analítica''', esto es, una ecuación que relacione las variables. | * Mediante una '''expresión analítica''', esto es, una ecuación que relacione las variables. | ||
| * Mediante una '''tabla''' que contenga los valores de las variables, emparejados. | * Mediante una '''tabla''' que contenga los valores de las variables, emparejados. | ||
| - | * Mediante una '''gráfica''', representada en unos '''ejes cartesianos''' con una escala adecuada. Sobre el eje horizontal (eje de '''abscisas''') representamos la variable independiente <math>x</math>, y sobre el eje vertical (eje de '''ordenadas''') la variable dependiente <math>y\;</math>. Cada punto de la gráfica es generado por una pareja de valores <math>x\;</math> e <math>y\;</math>, que son sus coordenadas <math>(x,y)\;</math>, su '''abcisa''' y su '''ordenada'''. | + | * Mediante una '''gráfica''', representada en unos '''ejes cartesianos''' con una escala adecuada. Sobre el eje horizontal (eje de '''abscisas''') representamos la variable independiente <math>x\;</math>, y sobre el eje vertical (eje de '''ordenadas''') la variable dependiente <math>y\;</math>. Cada punto de la gráfica es generado por una pareja de valores <math>x\;</math> e <math>y\;</math>, que son sus coordenadas <math>(x,y)\;</math>, su '''abcisa''' y su '''ordenada'''. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 56: | Línea 56: | ||
| [[Imagen:funcion_grifo_depot.png|300px|center]] | [[Imagen:funcion_grifo_depot.png|300px|center]] | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{wolfram desplegable|titulo=Formas de expresar una función|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Tabla de valores y gráfica de una función dada por una expresión analítica'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | En el ejemplo anterior hemos trabajado con la función V=2t: | ||
| + | |||
| + | :a) Obtén la tabla para t=0 hasta t=100 de 10 en 10. | ||
| + | :b) Dibuja la gráfica. | ||
| + | |||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=Table[2t,{t,0,100,10}]}} | ||
| + | :b) {{consulta|texto=Plot Table[2t,{t,0,100,10}]}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
Una función se puede expresar de varias formas:
- Mediante un enunciado que explique la relación que existe entre las variables.
- Mediante una expresión analítica, esto es, una ecuación que relacione las variables.
- Mediante una tabla que contenga los valores de las variables, emparejados.
- Mediante una gráfica, representada en unos ejes cartesianos con una escala adecuada. Sobre el eje horizontal (eje de abscisas) representamos la variable independiente
, y sobre el eje vertical (eje de ordenadas) la variable dependiente 
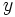. Cada punto de la gráfica es generado por una pareja de valores e 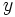, que son sus coordenadas 
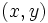, su abcisa y su ordenada.
Consideremos el ejemplo anterior del grifo y el depósito:
1. Enunciado:
- "Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."
2. Expresión analítica:
- t = "Tiempo que está abierto el grifo" (en segundos).
- V = "Volumen de agua que se ha llenado el depósito" (en litros).
3. Tabla de valores:
Tiempo (s) |
0 | 1 | 5 | 20 | 40 | 60 | 100 |
Volumen (l) |
0 | 2 | 10 | 40 | 80 | 120 | 200 |
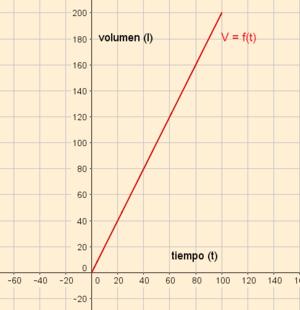
4. Gráfica:
- Representaremos los valores de la tabla en unos ejes de coordenadas. Cada punto de la gráfica consta de dos coordenadas: la primera es el valor de t y la segunda, el valor de V.
Actividad: Tabla de valores y gráfica de una función dada por una expresión analítica En el ejemplo anterior hemos trabajado con la función V=2t:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
