Divisibilidad de polinomios (4ºESO Académicas)
De Wikipedia
| Revisión de 17:20 13 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ===Polinomios múltiplos y divisores=== | + | {{Divisibilidad de polinomios}} |
| - | La divisibilidad en el conjunto de los polinomios es muy similar a la . | + | |
| - | {{p}} | + | ===Ejercicios propuestos=== |
| - | {{Caja_Amarilla|texto=Un polinomio <math>D(x)\,</math> es '''divisor''' de otro, <math>P(x)\,</math> y lo representaremos por <math>P(x)|Q(x)\;</math>, si la división <math>P(x):\,D(x)\,</math> es exacta. Es decir, cuando | + | {{ejercicio |
| - | {{p}} | + | |titulo=Ejercicios propuestos: ''Divisibilidad de polinomios'' |
| - | {{Caja|contenido=<math>P(x)=\,D(x)\cdot C(x)\,</math>}} | + | |cuerpo= |
| - | {{p}} | + | |
| - | En tal caso, diremos que <math>P(x)\,</math> es '''divisible''' por <math>Q(x)\,</math>. También diremos que <math>P(x)\,</math> es un '''múltiplo''' de <math>D(x)\,</math>. | + | (Pág. 45) |
| - | }} | + | |
| - | {{p}} | + | [[Imagen:red_star.png|12px]] 3, 5 |
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | |
| - | <math>(3x+1) \cdot (x^2-5x+3) =3x^3-14x^2+4x+3 \Rightarrow (3x^3-14x^2+4x+3):(3x+1)=x^2-5x+3</math> | + | [[Imagen:yellow_star.png|12px]] 1, 2, 4, 6 |
| - | }} | + | |
| - | La divisibilidad de polinomios es semejante a la [[Divisibilidad|divisibilidad con números enteros]]. Asimismo, la factorización de polinomios equivale a la descomposición de un número en factores primos, y los conceptos de '''máximo común divisor''', '''mínimo común múltiplo''' e '''irreducibilidad''' son similares a los correspondientes conceptos numéricos. | + | |
| - | {{p}} | + | |
| - | ==Polinomios irreducibles== | + | |
| - | {{Caja_Amarilla|texto=Un polinomio <math>P(x)\,</math> es '''irreducible''' cuando ningún polinomio de grado inferior es divisor suyo.}} | + | |
| - | {{p}} | + | |
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | |
| - | Son polinomios irreducibles, entre otros: | + | |
| - | * Los de primer grado: <math>3x,\ x-3,\ 5x-3\ \cdots \;</math> | + | |
| - | * Los de segundo grado sin raíces: <math>x^2+1,\ 2x^2-3x+5 \cdots \;</math> | + | |
| }} | }} | ||
| + | |||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Calculadora |
Tabla de contenidos |
Polinomios múltiplos y divisores
- Un polinomio
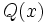 es divisor de otro,
es divisor de otro, 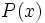 y lo representaremos por
y lo representaremos por 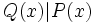 , si la división
, si la división 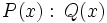 es exacta, es decir, cuando existe otro polinomio
es exacta, es decir, cuando existe otro polinomio 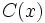 tal que
tal que 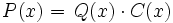 .
.
- En tal caso, diremos que
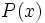 es divisible por
es divisible por 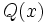 y que
y que 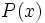 es un múltiplo de
es un múltiplo de 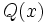 .
.
- También diremos que
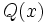 y
y 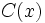 son factores del polnomio
son factores del polnomio 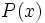 .
.
Dados los polinomios:
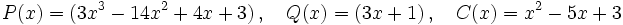 :
:Se cumple que
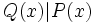 , porque
, porque 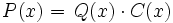 .
.Es decir, la siguiente división es exacta:
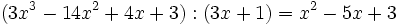
porque:
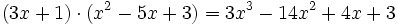
La divisibilidad de polinomios es semejante a la divisibilidad con números enteros. Asimismo, la factorización de polinomios equivale a la descomposición de un número en factores primos, y los conceptos de máximo común divisor, mínimo común múltiplo e irreducibilidad son similares a los correspondientes conceptos numéricos.
Polinomios irreducibles
Un polinomio 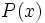 es irreducible cuando ningún polinomio de grado inferior (distinto de grado cero) es divisor suyo.
es irreducible cuando ningún polinomio de grado inferior (distinto de grado cero) es divisor suyo.
Son polinomios irreducibles, entre otros:
- Los de primer grado:
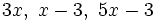
- Los de segundo grado sin raíces:
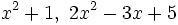
Máximo común divisor y mínimo común múltiplo
Se dice que el polinomio 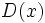 es el máximo común divisor de los polinomios
es el máximo común divisor de los polinomios 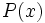 y
y 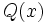 , y lo expresaremos:
, y lo expresaremos:
![m.c.d \,[P(x), Q(x)]=D(x)\;](/wikipedia/images/math/c/6/6/c66f3168e53561a04ed46aade0f24ca0.png)
si 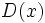 es divisor de ambos y no existe otro polinomio que divida a ambos que tenga mayor grado que él.
es divisor de ambos y no existe otro polinomio que divida a ambos que tenga mayor grado que él.
Se dice que el polinomio 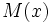 es el mínimo común múltiplo de los polinomios
es el mínimo común múltiplo de los polinomios 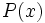 y
y 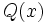 , y lo expresaremos:
, y lo expresaremos:
![m.c.m \,[P(x), Q(x)]=M(x)\;](/wikipedia/images/math/2/2/1/221e514439439421dc1201091dd735b3.png)
si 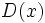 es múltiplo de ambos y no existe otro polinomio que sea múltiplo de ambos que tenga menor grado que él.
es múltiplo de ambos y no existe otro polinomio que sea múltiplo de ambos que tenga menor grado que él.
Ejercicios propuestos
|
Ejercicios propuestos: Divisibilidad de polinomios |
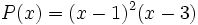
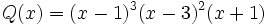 :
:
![m.c.d \,[P(x), Q(x)]=(x-1)^2(x-3)\;](/wikipedia/images/math/9/6/c/96c02ce39375f7c1585c25c27c0c0fcb.png)
![m.c.m \,[P(x), Q(x)]=(x-1)^3 (x-3)^2 (x+1)\;](/wikipedia/images/math/8/d/5/8d598eb8a1613c40ffc2eebba001fa1f.png)

