Semejanza de triángulos
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 21:18 19 dic 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 21:31 19 dic 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 22: | Línea 22: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==Triángulos en la posición de Tales== | ||
| + | {{Caja_Amarilla | ||
| + | |texto= | ||
| {{Tabla75 | {{Tabla75 | ||
| - | |celda1=Si las rectas a, b, c son paralelas y cortan a otras dos rectas r y s, entonces los segmentos que determinan en ellas son proporcionales. | + | |celda1=Dos triángulos ABC y A'B'C', con sus lados paralelos y encajados con un vértice común, se dice que están en la '''posición de [[Tales de Mileto|Tales]]''' |
| - | |celda2=[[Imagen:Ejemplo.jpg]] | + | |celda2=[[Imagen:triangulos_tales.png]] |
| }} | }} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| {{Desplegable | {{Desplegable | ||
| |titulo=Explicación: | |titulo=Explicación: | ||
Revisión de 21:31 19 dic 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Semejanza | WIRIS Geogebra Calculadora |
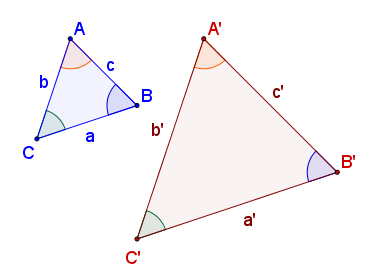
Triángulos semejantes
Triángulos en la posición de Tales
| Dos triángulos ABC y A'B'C', con sus lados paralelos y encajados con un vértice común, se dice que están en la posición de Tales | 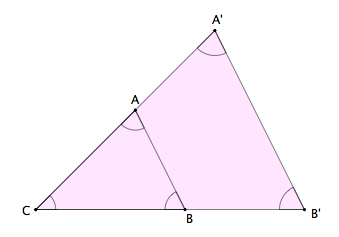
|
Explicación:
|
Actividad Interactiva: Figuras semejantes
1. Comprueba las propiedades de dos figuras semejantes.
Actividad: Observa los dos polígonos de la figura. Se dice que son semejantes porque cumplen las dos condiciones antes mencionadas:
En efecto, 1. Los ángulos son iguales ya que los lados correspondientes son paralelos. 2. Para comprobar que los lados son proporcionales usa los segmentos MN y XY que puedes mover libremente. Mide con ellos dos segmentos correspondientes AB y A'B' por ejemplo y calcula la razón de semejanza. Mueve ahora el punto rojo para comprobar el valor de r. |
Escala
Ya hemos visto antes que escala y razón de semejanza significan lo mismo. El término escala suele utilizarse en planos o mapas. Así, por ejemplo, decimos que un plano está a escala 1:100 si 1 cm en el plano son 10 cm en la realidad. Es lo mismo que decir que la razón de semejanza entre la figura dibujada y la real es 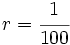 .
.
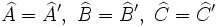
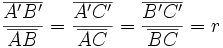
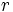 , se la razón de semejanza.
, se la razón de semejanza.