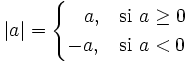Valor absoluto (PACS)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:48 27 sep 2008 Juanmf (Discusión | contribuciones) (→Valor absoluto de un número real) ← Ir a diferencia anterior |
Revisión actual Juanmf (Discusión | contribuciones) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | == Valor absoluto de un número real == | + | ==Definición == |
| - | + | {{Caja Amarilla | |
| + | |texto= | ||
| + | [[Imagen:Absolute value.png|thumb|right|230px|Gráfica de la función ''valor absoluto'']] | ||
| Formalmente, el '''valor absoluto''' o '''módulo''' de todo número real <math> \ a </math> y con la notación <math>|\ a |</math> (introducida por Karl Weierstrass en 1841), está definido por: | Formalmente, el '''valor absoluto''' o '''módulo''' de todo número real <math> \ a </math> y con la notación <math>|\ a |</math> (introducida por Karl Weierstrass en 1841), está definido por: | ||
| Línea 18: | Línea 20: | ||
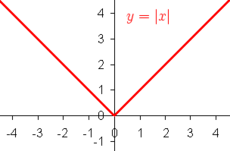
| Desde un punto de vista geométrico, el valor absoluto de un número real <math>a</math> corresponde a la distancia a lo largo de la recta numérica real desde <math>a</math> hasta el número cero. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. | Desde un punto de vista geométrico, el valor absoluto de un número real <math>a</math> corresponde a la distancia a lo largo de la recta numérica real desde <math>a</math> hasta el número cero. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. | ||
| + | }} | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://www.maralboran.org/web_ma/descartes/Analisis/funcion_valor_absoluto_mgb/mogebo_absolut.htm | ||
| + | width=100% | ||
| + | height=2100 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
Revisión actual
Menú:
| Enlaces internos | Para repasar | Enlaces externos |
| Indice CD Alumno 07 Resueltos 07 Descartes Manual Casio | WIRIS Calculadora |
[editar]
Definición
Formalmente, el valor absoluto o módulo de todo número real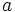 
y con la notación 
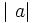(introducida por Karl Weierstrass en 1841), está definido por:
Note que por definición el valor absoluto de a siempre será mayor o igual que cero, y nunca negativo.
Desde un punto de vista geométrico, el valor absoluto de un número real a corresponde a la distancia a lo largo de la recta numérica real desde a hasta el número cero. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos.
