Fórmula del binomio de Newton (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:01 4 sep 2016 Coordinador (Discusión | contribuciones) (→Triángulo de Pascal) ← Ir a diferencia anterior |
Revisión de 19:01 4 sep 2016 Coordinador (Discusión | contribuciones) (→Triángulo de Pascal) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| ===Triángulo de Pascal=== | ===Triángulo de Pascal=== | ||
| {{Tabla75|celda2= | {{Tabla75|celda2= | ||
| - | [[Imagen:Triangulo_Pascal.png|thumb|210px|Triángulo de Pascal para ''n=10''.]] | + | [[Imagen:Triangulo_Pascal.png|thumb|240px|Triángulo de Pascal para ''n=10''.]] |
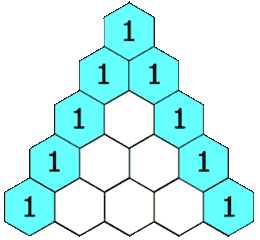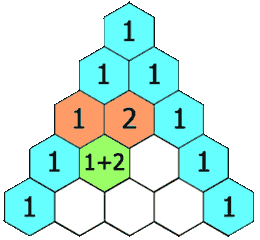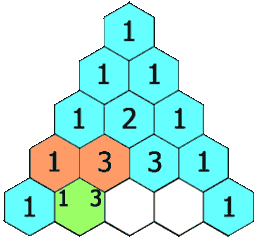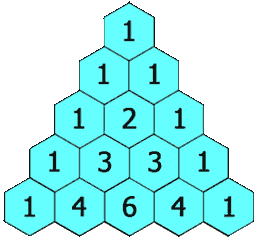
| <center>[[Imagen:Triangulo_Pascal_1.gif|Triángulo de Pascal para ''n=3''.]]</center> | <center>[[Imagen:Triangulo_Pascal_1.gif|Triángulo de Pascal para ''n=3''.]]</center> | ||
| |celda1= | |celda1= | ||
Revisión de 19:01 4 sep 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Binomio de Newton
Teorema: Fórmula del binomio de Newton
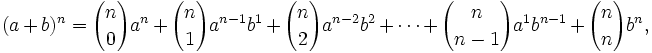
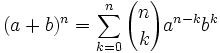
|
Triángulo de Pascal
|
El triángulo de Pascal es una representación de los coeficientes binomiales 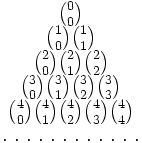 También conocido como triángulo de Tartaglia, especialmente en Italia, en honor al algebrista italiano Niccolò Fontana Tartaglia (1500–77).
Propiedades
Demostración:
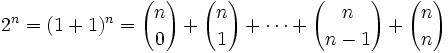
|
|
Actividad: Binomio de Newton
Solución: Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión:
|
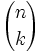 , los
, los 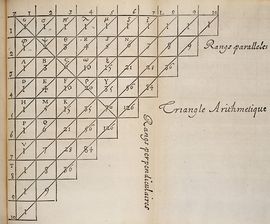
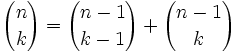 . [1]
. [1]
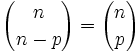 . [2]
. [2]