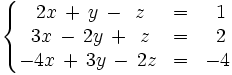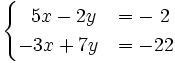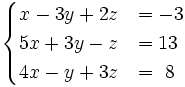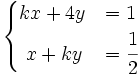Regla de Cramer (2ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:20 29 sep 2019 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 5: | Línea 5: | ||
| |sinopsis=Regla de Crammer para resolver sistemas de ecuaciones | |sinopsis=Regla de Crammer para resolver sistemas de ecuaciones | ||
| }} | }} | ||
| + | ---- | ||
| {{Video_enlace_pildoras | {{Video_enlace_pildoras | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| Línea 48: | Línea 49: | ||
| :<math>\begin{cases}kx+4y & = 1 \\ ~x+ky & = \cfrac{1}{2} \end{cases}</math> | :<math>\begin{cases}kx+4y & = 1 \\ ~x+ky & = \cfrac{1}{2} \end{cases}</math> | ||
| |url1=https://www.youtube.com/watch?v=DO_UttzvefU&index=107&list=PL9B9AC3136D2D4C45 | |url1=https://www.youtube.com/watch?v=DO_UttzvefU&index=107&list=PL9B9AC3136D2D4C45 | ||
| + | }} | ||
| + | {{Video_enlace_miguematicas | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=7'34" | ||
| + | |sinopsis=Resuelve utilizando la regla de Cramer: | ||
| + | |||
| + | <math> | ||
| + | \left\{ \begin{matrix} | ||
| + | ~2x \, + \, y \, - \, ~z & = & ~1 | ||
| + | \\ | ||
| + | ~3x \, - \, 2y \, + \, ~z & = & ~2 | ||
| + | \\ | ||
| + | -4x \, + \, 3y \, - \, 2z & = & -4 | ||
| + | \end{matrix} | ||
| + | \right. | ||
| + | </math> | ||
| + | |url1=https://youtu.be/wWiyswAREwA?list=PLLfTN7MHLxConbepI-_1OEy-pjAxI8IvH | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
Regla de Crammer para resolver sistemas de ecuaciones
Resuelve utilizando la regla de Cramer:
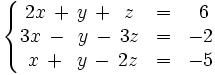
Resuelve mediante la regla de Cramer:
Resuelve mediante la regla de Cramer:
Halla el valor de "k" para que el sistema sea compatible determinado:
Resuelve utilizando la regla de Cramer: