Semejanza de triángulos
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 21:47 19 dic 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 22:02 19 dic 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 18: | Línea 18: | ||
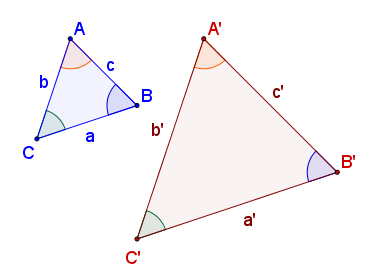
| donde <math>r\;\!</math>, se la '''razón de semejanza'''. | donde <math>r\;\!</math>, se la '''razón de semejanza'''. | ||
| - | |celda2=<center>[[Imagen:triangulos_semejantes.png]]</center> | + | |celda2=<center>[[Imagen:triangulos_semejantes.png|420px]]</center> |
| }} | }} | ||
| }} | }} | ||
| Línea 32: | Línea 32: | ||
| <center><math> \frac {\overline{OA'}} {\overline{OA}} = \frac {\overline{OB'}} {\overline{OB}}</math></center> | <center><math> \frac {\overline{OA'}} {\overline{OA}} = \frac {\overline{OB'}} {\overline{OB}}</math></center> | ||
| |celda2= | |celda2= | ||
| - | <center>[[imagen:teorema_de_Tales_1.png|primer teorema de Tales]]</center> | + | <center>[[imagen:teorema_de_Tales_1.png|470px]]</center> |
| }} | }} | ||
| |demo= | |demo= | ||
Revisión de 22:02 19 dic 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Semejanza | WIRIS Geogebra Calculadora |
Triángulos semejantes
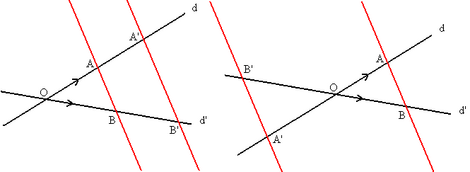
Teorema de Tales
Teorema de Tales
Dos rectas d y d', que se cortan en un punto O, cortadas por rectas paralelas AB y A'B', determinan segmentos proporcionales:
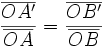 |
Demostración:
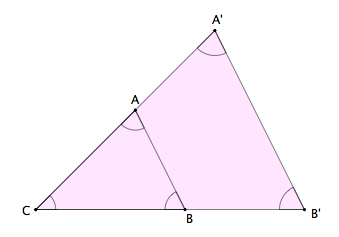
Triángulos en la posición de Tales
| Dos triángulos ABC y A'B'C', con sus lados paralelos y encajados con un vértice común, se dice que están en la posición de Tales |
Proposición:Triángulos en la posición de Tales
Dos triángulos son semejantes si y sólo si están en la posición de Tales.
Demostración:
Observa la siguiente escena y mueve el punto verde para desplazar el triángulo amarillo. Podrás comprobar que los ángulos son iguales
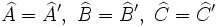
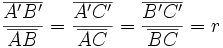
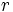 , se la razón de semejanza.
, se la razón de semejanza.