Fórmula del binomio de Newton (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:10 18 sep 2016 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) ← Ir a diferencia anterior |
Revisión de 11:10 18 sep 2016 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) Ir a siguiente diferencia → |
||
| Línea 95: | Línea 95: | ||
| (Pág. 45) | (Pág. 45) | ||
| [[Imagen:red_star.png|12px]] 1a | [[Imagen:red_star.png|12px]] 1a | ||
| + | |||
| [[Imagen:yellow_star.png|12px]] 1b,c; 2 | [[Imagen:yellow_star.png|12px]] 1b,c; 2 | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Números|Reales]] | [[Categoría: Matemáticas]][[Categoría: Números|Reales]] | ||
Revisión de 11:10 18 sep 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(pág 45)
Binomio de Newton
Teorema: Fórmula del binomio de Newton El desarrollo de la potencia n-ésima de un binomio viene dado por la siguiente fórmula:
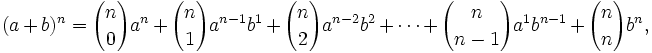
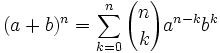 siendo
|
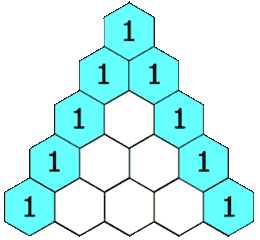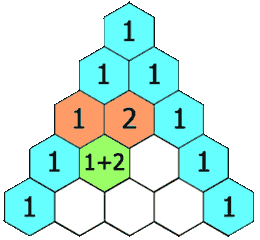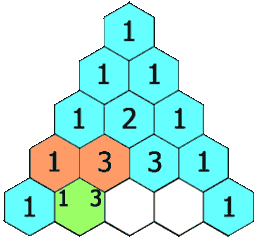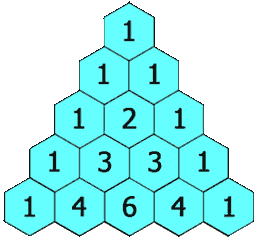
Triángulo de Pascal
|
El triángulo de Pascal es una representación de los coeficientes binomiales ordenados en forma triangular. 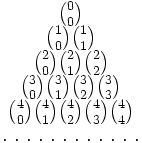 También conocido como triángulo de Tartaglia, especialmente en Italia, en honor al algebrista italiano Niccolò Fontana Tartaglia (1500–77).
Propiedades
Demostración:
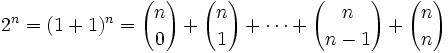
|
Ejercicios propuestos
|
Ejercicios propuestos: Binomio de Newton |
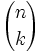 , los
, los 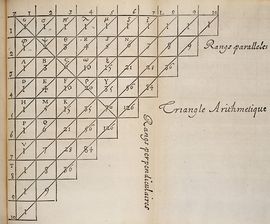
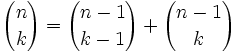 . [1]
. [1]
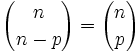 . [2]
. [2]