Plantilla:Cálculo de la pendiente de y=mx
De Wikipedia
| Revisión de 19:48 7 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:56 7 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| La pendiente de una función de proporcionalidad directa se puede hallar de la siguiente manera: | La pendiente de una función de proporcionalidad directa se puede hallar de la siguiente manera: | ||
| - | {{Teorema_|titulo=Proposición|enunciado=Consideremos una función de proporcionalidad directa <math>y=m \cdot x\;</math>, y sea <math>A(x_1,y_1)\;</math>, con <math>x_1 \ne 0</math>, un punto de la recta que la representa, entonces | + | {{Teorema_|titulo=Proposición|enunciado=Consideremos una función de proporcionalidad directa <math>y=m x\;</math> y un punto <math>A(x_1,y_1)\;</math> de la recta que la representa, distinto del origen. Se cumple que: |
| <center><math>m=\cfrac {y_1}{x_1}</math></center> | <center><math>m=\cfrac {y_1}{x_1}</math></center> | ||
Revisión de 19:56 7 nov 2016
La pendiente de una función de proporcionalidad directa se puede hallar de la siguiente manera:
Proposición
Consideremos una función de proporcionalidad directa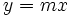 
y un punto 
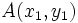de la recta que la representa, distinto del origen. Se cumple que:
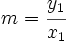
Es inmediato, pués si 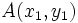es un punto de la recta 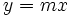, cumplirá su ecuación:
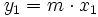
Despejando, tenemos:
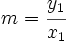
En esta escena podrás ver como se calcula la pendiente de una función de proporcionalidad directa y como se obtiene su ecuación.
Autoevaluación: Cálculo de la pendiente Descripción: Consideremos la función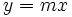 
, cuya pendiente es 
.
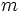La pendiente de una recta tiene mucha relación con las coordenadas de los puntos por donde pasa.
En la siguiente escena tienes que seleccionar el número que corresponde a la pendiente de la recta azul fijándote en las coordenadas del punto rojo de la recta.
Para dar valores a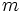 
puedes escribir números decimales o fracciones como 5/7 ó -1/2 y pulsar la tecla Intro.
Si aciertas verás la expresión de la función con color azul, si no aciertas verás la recta correspondiente de color rojizo. Después de cada acierto pulsa el botón "animar" para que salga una nueva recta.
Actividad: Función de proporcionalidad directa
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
